Тема урока: Свойства и признаки равнобедренного треугольника
Ход урока:

1. Устная работа с чертежами
(раздаточный материал – в Приложении 1): нужно выбрать номера чертежей, которые иллюстрируют
- четыре определения;
- три свойства равнобедренного треугольника;
- три признака равнобедренного треугольника.
ОТВЕТЫ:
(1) определения – на рис. 2; 4; 7; 9;
(2) свойства – на рис. 6; 8; 10;
(3) признаки – на рис. 1; 3; 5.
2. Деление на группы
(три группы по 7 человек), придумывание название группы.
3. Диктант на дружбу
(по очереди каждый член команды (посыльный) подходит к учителю, несколько минут читает формулировку того или иного утверждения и затем диктует это утверждение членам команды; всего – десять утверждений – см. Приложение 2);
та команда, которая первой дружно хлопнет в ладоши, записав очередную формулировку, получает в таблице баллов на доске два «плюса», та, что вторыми закончит записи, — один «плюс», та, что заканчивает записи последней, — ни одного плюса.

4. Взаимная проверка диктанта
(по часовой стрелке группы перемещаются и сверяют записи в тетрадях соперников; в таблице баллов на доске в виде «минусов» ставится количество различий в тетрадях членов одной команды; соответственно два «минуса» впоследствии «уничтожат» один «плюс», а команда, набравшая большее число баллов-«плюсов» получит бонус в виде повышения на балл оценки за работу на уроке).

5. Добавление к записанным в тетрадях утверждениям поясняющих рисунков
(каждый учащийся выбирает из ШАПКИ ВОПРОСОВ чей-то листочек с рисунками и ответами к ним и с его помощью записывает около каждого утверждения НОМЕР иллюстрирующего его чертежа).

Повторная проверка по ЭТАЛОНАМ учителя (команды снова «идут в гости» к другой команде, взяв предварительно листочек с ЭТАЛОНОМ, проверяют соответствие рисунка утверждению и по критериям, записанным на доске, выставляют каждому учащемуся ОЦЕНКУ за работу на уроке; ЭТАЛОНЫ – в Приложении 3).

В завершении урока командам предлагается сбрать «пазлы» с самыми главными теоремами, необходимыми для доказательства всех свойств и признаков равнобедренного треугольника, – ПРИЗНАКАМИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ (см. Приложение 4), та команда, кто первой соберет «пазлы» в формулировку одного из трех признаков равенства треугольников, хором говорит название ПРИЗНАКА и если успевает, — инсценирует ПРИЗНАК.

По окончании урока учитель собирает тетради и выставляет за урок среднее арифметическое из следующих оценок:
- за домашнее задание;
- за устную работу в начале урока;
- за тексты формулировок, записанных учащимся под диктовку членов его группы;
- за соответствие рисунков записанным утверждениям.

Приложение 1.
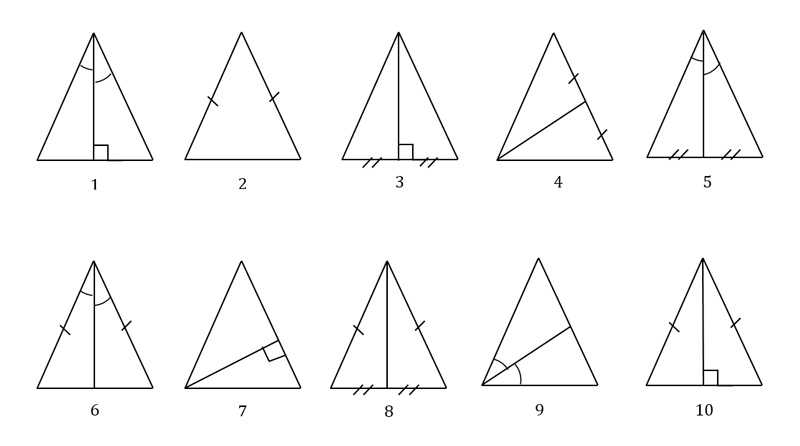
Запиши номера рисунков, которые иллюстрируют:
1) определения (определение равнобедренного треугольника, медианы треугольника, биссектрисы треугольника и высоты треугольника):____________________________
2) свойства равнобедренного треугольника:___________________________________
3) признаки равнобедренного треугольника:___________________________________
(каждый рисунок иллюстрирует ТОЛЬКО ОДНО утверждение)
Приложение 2.
Опр. 1: треугольник называется равнобедренным, если две его стороны равны.
Опр. 2: медианой треугольника называется отрезок, соединяющий вершину с серединой противолежащей стороны.
Опр. 3: биссектрисой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне, который делит угол треугольника на два равных угла.
Опр. 4: высотой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне или ее продолжении, который перпендикулярен стороне треугольника.
Свойство 1: биссектриса равнобедренного треугольника, проведенная к его основанию, является и медианой треугольника, и его высотой.
Свойство 2: медиана равнобедренного треугольника, проведенная к его основанию, является и биссектрисой треугольника, и его высотой.
Свойство 3: высота равнобедренного треугольника, проведенная к его основанию, является и медианой треугольника, и его биссектрисой.
Признак 1: если высота треугольника является его медианой, то этот треугольник равнобедренный.
Признак 2: если биссектриса треугольника является его высотой, то этот треугольник равнобедренный.
Признак 3: если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный.
Приложение 3
Опр.1: треугольник называется равнобедренным, если две его стороны равны.
Рис. 2
Опр 2: медианой треугольника называется отрезок, соединяющий вершину с серединой противолежащей стороны.
Рис. 4
Опр. 3: биссектрисой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне, который делит угол треугольника на два равных угла.
Рис. 9
Опр. 4: высотой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противолежащей стороне или ее продолжении, который перпендикулярен стороне треугольника.
Рис. 7
Свойство 1: биссектриса равнобедренного треугольника, проведенная к его основанию, является и медианой треугольника, и его высотой.
Рис. 6
Свойство 2: медиана равнобедренного треугольника, проведенная к его основанию, является и биссектрисой треугольника, и его высотой.
Рис. 8
Свойство 3: высота равнобедренного треугольника, проведенная к его основанию, является и медианой треугольника, и его биссектрисой.
Рис. 10
Признак 1: если высота треугольника является его медианой, то этот треугольник равнобедренный.
Рис. 3
Признак 2: если биссектриса треугольника является его высотой, то этот треугольник равнобедренный.
Рис. 1
Признак 3: если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный.
Рис. 5
Приложение 4
- Если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника, то такие треугольники равны.
- Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.




