В.М.Букатов, доктор педагогических наук, профессор МПСУ,
научный руководитель экспериментальных площадок
по социо-игровой педагогике:
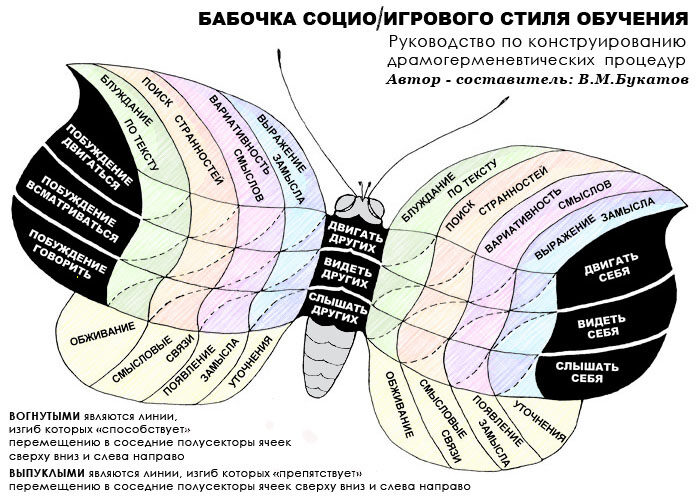
О ТАБЛИЦЕ-БАБОЧКЕ СОЦИО-ИГРОВОГО СТИЛЯ ОБУЧЕНИЯ И ДРАМОГЕРМЕНЕВТИЧЕСКОЙ ПОВСЕДНЕВНОСТИ НА ШКОЛЬНЫХ УРОКАХ
Перечень статей, поясняющих драмогерменевтическую таблицу-БАБОЧКУ
- Наглядная система профессиональных подсказок, адресованных интуиции учителя открыть в новом окне
- Три социо-игровых постулата педагогического мастерства открыть в новом окне
- О герменевтических подходах к пониманию открыть в новом окне
- Групповая коммуникативность как один из секретов успешности обучения открыть в новом окне
- Процедурная драматургия герменевтической «цепочки понимания» открыть в новом окне
- Прокрустово ложе творческого самовыражения открыть в новом окне
- О профессиональных подоплёках табличных построений открыть в новом окне
- Соблюдение последовательности как показатель профессионализма открыть в новом окне
4. Групповая коммуникативность как один из секретов успешности обучения
4.1. Уникальный потенциал случайных по составу малых групп
4.2. Когда ученическая «разношерстность» идет всем на пользу
Многие школьные методики предлагают учителю какие-то свои особые рецепты того, как ему на уроке обеспечить каждого ученика полноценно-деловой занятостью. Есть такой рецепт и в социо-игровой педагогике: почаще организовывать на своих уроках работу малых групп.То есть таких временных рабочих группок-команд-бригад, численность которых колеблется от трёх человек до восьми (эффективность этого диапазона легко подтверждается эмпирически).
Создаются эти ситуативные группы, как правило, с помощью игровой жеребьевки. Непредсказуемость результата объединения в малые группы для социо-игрового стиля обучения принципиальна, так как «игровая случайность» несет в себе уникальную воспитательную — а точнее, психотерапевтическую! — функцию.
4.1. Уникальный потенциал случайных по составу малых групп
Незамысловатые детские считалочки гарантированно обеспечивают случайность выбора, которая устраивает большинство детей, помогая им легко и быстро сплотиться внутри получившихся групп. Сплочение это происходит как бы впопыхах, на скорую руку, что уже является весьма неплохим коммуникативным результатом. Поэтому учителю после того, как он с помощью игровых приемов обеспечит «самозарождение» в учениках деловой увлеченности, остается всего-то на всего не мешать дальнейшей взаимной возгонке, сопряжению и обогащению этой самой детской увлеченности.
Подчеркнем, что общая увлеченность класса стимулирует в каждой команды внутреннюю коммуникативность. Общение в малой группке становится все более и более неформальным. Совместная деятельность группки учеников (даже если кто-то из них занят, казалось бы, только чем-то своим) позволяет им понимать друг друга «с полуслова». А это в свою очередь создает весьма благоприятные условия для стихийного обмена информацией (мнениями, установками, ситуационными открытиями, накопленными пониманиями, эмоциональными и поведенческими наработками).
Правда, для стороннего наблюдателя (например, для учителя, ведущего урок) этот обмен оказывается весьма закрытым, непрозрачным, мало предсказуемым и практически не контролируемым. Обычно это приводит некоторых учителей к мысли, что лучше обходить подобные ситуации стороной, «от греха подальше». Раз свой нос сунуть нельзя, то и нечего вольницу устраивать: вдруг они там «малину» разведут — начинает пугать себя иной учитель. И совершенно зря…
Учителям-перестраховщикам драмо/герменевтическая бабочка помогает успокоиться. Потому что, как в горизонтальной маркировке (что находится в верхних и нижних колонтитулах), так и в маркировке вертикальной (что расположена на тёмном фоне), размещены подсказки учителю, какие варианты деловых перспектив могут заинтересовать (или уже заинтересовали) учеников в ходе их совместного выполнения в своих малых группах полученного задания.
Особо подчеркнем, что система маркировки подталкивает учителя к тому, чтобы он на определенных этапах урока (а именно во время «пиков» увлечённости малых группок своей работой над заданием) начал налаживать между ними деловито-игровую коммуникативность. Тогда развитие процесса неформально-делового общения внутри группок ускоряется (или подстегивается), наполняя жизнь каждого ученика на данном уроке эмоционально-интеллектуальными впечатлениями насыщенности и полноценности проживаемых ситуаций…
4.2. Когда ученическая «разношерстность» идет всем на пользу
Ранее было сказано, что таблица-БАБОЧКА, помимо всего прочего, причудливо отражает возможные варианты ученических перспектив личной деятельности. Добавим, что вариативность эта становится для каждого из учеников наиболее актуальной, когда все они начинают на уроке работать в условиях малых групп.
Получается, что таблица может сподвигнуть учителя на изобретение для своего очередного урока такой режиссуры, которая погружала бы в деловую занятость не просто какого-то среднеарифметического ученика, а всех тех реальных и разношерстных детей, что учатся в конкретном классе. И начнется такая режиссура с того, что на определенном этапе урока класс разойдется по каким-то малым группкам (очередной раз подчеркнем: в строго непредсказуемо-игровом порядке).
Итак, вместо привычного фронтального задания классу для индивидуального выполнения (с последующим неизбежным отчитыванием нерадивых, нарушающих стройность фронтальной линии качественности современного обучения) социо-игровой стиль обучения предлагает учителю сначала объединить учеников в несколько «малых группок», а затем каждой из них дать одно и тоже задание (это чтобы ученикам было сподручно сравнивать, судить и делать комплексные выводы и об изучаемом материале, и друг о друге, и о самих себе).
Подобная «режиссура урока» оказывается гораздо эффективней, чем проведение, например, фронтальной проверки со всеми обычно присущими ей дисциплинарными инсталляциями (как со стороны учителя, так и со стороны учеников), суровым (или истеричным) разбором допущенных ошибок и формальным (или тенденциозно заинтересованным) выявлением «победителей».
И заметьте, что работа малых группок «случайного состава» (особо подчеркнем, что случайной не только для учеников, но и для учителя), как и ученические впечатления о деловой насыщенности урока, не находятся в прямой зависимости от успеваемости самих этих учеников, от их ранее проявленных способностей и уже существовавших у них интересов (что для педагогики весьма важно). На таком уроке и слабый ученик может наконец-то вкусить радость победы и чувство окрыления от делового успеха группы.
Да и сильного ученика могут ждать свои сюрпризы — например, неожиданная горечь поражения, которая для его личного опыта может оказаться весьма полезным приобретением. Как показывает опыт многих учителей, выбравших социо-игровой стиль обучения, ученическая «разношерстность» в классах просто-таки необходима, потому что именно она лучше всего приводит к появлению в классе тотальной эмоциональной установки на всестороннюю креативность.
Таблица-БАБОЧКА позволяет учителям не только внутренне подготовиться к тем предлагаемым обстоятельствам урока, о которых в методической литературе обычно предпочитают особо не распространяться, но и поворачивать их в выгодную для обучения сторону. Открывать же глаза на эти самые предлагаемые обстоятельства и считаться с ними нам помогает герменевтика. Это она напоминает нам, что субъективность эффекта понимания с одной стороны неизбежна, а с другой непредсказуема — таково естество человека, с которым любому учителю лучше считаться как с самым главным определяющим обстоятельством своей профессиональной деятельности. Оно требует вести свои уроки так, чтобы любой из присутствующих детей, обнаружив свою «точку непонимания», в любой момент занятия мог бы не только обогащаться каким-то личным открытием, но и свободно поделиться им со своими столь же неравнодушными соседями (при этом невольно сравнивая значимость своей находки, понимания и открытия со значимостью соседских находок, пониманий и открытий). Это создает самые сказочные условия для продвижения каждого из учеников в свою собственную «зону ближайшего развития» (по Выготскому).
Для того, чтобы подобные ситуации как можно чаще возникали в повседневности и начальной, и средней, и даже старшей школы (причем на уроках по любой из учебных дисциплин), и была создана драмогерменевтическая БАБОЧКА.
Педагогическая составляющая драмогерменевтики
Нередко учитель искренне желает быть отзывчивым, но не замечает, что инициативу на уроке отдает не вовремя, «дистанцию» во взаимоотношениях не меняет, в демонстрации своих сил несдержан, а в поиске общих интересов (или в следовании им) неустойчив…
Герменевтическая составляющая драмогерменевтики
Когда количество странностей начинает превышать «критическую массу», для субъекта наступает их взаиморазрешение новым смыслом. Странности исчезают, уступая место новому пониманию, более углубленному, детальному, эмоционально обновленному…
Театральная составляющая драмогерменевтики
Во время репетиции актеры в поисках «зерна» роли совершают великое множество попутных действий. Зрители же на спектакле, как и ученики на уроке, живут гораздо пассивнее, так как ограничены в совершении попутных действий…

О трёх составляющих драмогерменевтики
Освоение драмогерменевтики неизбежно связано с накоплением личного педагогического и жизненного опыта. Чем старше педагог, тем более связно могут формироваться его представления о драмогерменевтике
О педагогике, как реально практикующем искусстве
Совершенствование своего собственного поведения освобождает учителя от многих абстрактно-педагогических разговоров о дидактических и воспитательных целях, задачах и методах. Сущность такого освобождения мы и определяем составным термином драмогерменевтика.
Блуждание по картинке
Блуждание по картинке один из социо-игровых приёмов Родной педагогики для углублённого изучения и понимания изображений. В помощь взрослым для обучения детей глубокому и осмысленному пониманию, развитию своего видения. Для изучения новых учебных материалов. Для знакомства и изучения искусства. Для интересных уроков.
8. Соблюдение последовательности как показатель профессионализма
Некоторые дети весьма чутко реагируют даже на малейшие нарушения учителем той естественности, которая присуща самому протеканию многоступенчатого процесса понимания. Поэтому специально для учителей эта естественность зафиксирована в последовательности герменевтических процедур.
7. О профессиональных подоплёках табличных построений
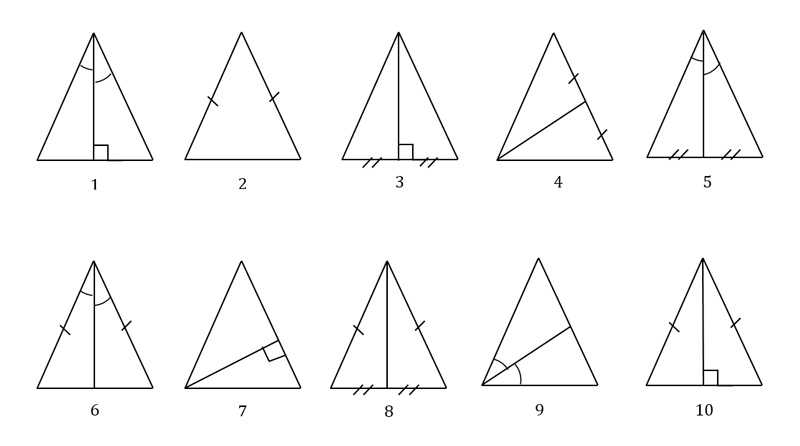
Ученическое продвижение по треугольничкам, как можно сказать и будет являться самым настоящим образовательным путешествием. Оно обычно происходит скачкообразно и непоследовательно. И у каждого ребенка траектория путешествия оказывается индивидуальной.
6. Прокрустово ложе творческого самовыражения
Последнее звено в цепочке процедурных приемов, связанных с пониманием текста, — выражение замысла. Некоторые учителя упорно называют это звено «творческим»
5. Процедурная драматургия герменевтической «цепочки понимания»
В социо-игровой герменевтике существует так называемая процедурная цепочка неких взаимосвязанных приемов, приводящих к личностному пониманию сложного, непривычного, пугающего своей новизной текста. На БАБОЧКЕ эта цепочка воспроизведена дважды: на правом крылышке и на левом.
4. Групповая коммуникативность как один из секретов успешности обучения
Многие школьные методики предлагают учителю какие-то свои особые рецепты того, как ему на уроке обеспечить каждого ученика полноценно-деловой занятостью. Есть такой рецепт и в социо-игровой педагогике: почаще организовывать на своих уроках работу малых групп.
3. О герменевтических подходах к пониманию
Начнем с того, что когда ученик говорит:«А, всё ясно!» — и машет рукой, это вовсе не значит, что он действительно все понял. Равнодушное махание рукой к пониманию не ведет и понимания не обеспечивает.
Наглядная система профессиональных подсказок
В.М.Букатов, доктор педагогических наук, профессор МПСУ, научный руководитель экспериментальных площадок по социо-игровой педагогике: О ТАБЛИЦЕ-БАБОЧКЕ СОЦИО-ИГРОВОГО СТИЛЯ ОБУЧЕНИЯ И ДРАМОГЕРМЕНЕВТИЧЕСКОЙ ПОВСЕДНЕВНОСТИ НА ШКОЛЬНЫХ УРОКАХ 1. Наглядная система профессиональных подсказок, адресованных интуиции учителя: 1.1. Плавные контуры летающей симпатяги 1.2. О вертикальной и горизонтальной маркировке Обращаем особое внимание — системой подсказок, а не очередной методичкой-инструкцией, наподобие тех, […]

Драмогерменевтическая таблица-БАБОЧКА
Наглядная система профессиональных подсказок, адресованных интуиции учителя. Основная задача таблицы-БАБОЧКИ — обеспечить учителей системой наглядных подсказок: какие именно из известных им методических социо-игровых приемов имеет смысл использовать, организовывать и проводить на своих ближайших уроках.
Дидактические перспективы: от социо-игрового стиля обучения к драмогерменевтике
В герменевтике — науке об искусстве понимания — констатируется, что в книгах читатель может найти или пищу для размышления над уже знакомыми и доступными проблемами, или подтверждение правильности своих решений, уже ранее найденных.