КУБИЧЕСКИЕ ЗДАНИЯ
дидактический блок методики Хейни
автор: Милан ХЕЙНИ
перевод с чешского: Светлана ФРИГА
Развитие пространственного воображения
Кубические здания — Этот дидактический блок опирается на опыт детей игры с кубиками, легко интегрируется в процесс изучения арифметики и очень способствует развитию пространственного воображения.
Правила и определения
Что считать КУБИЧЕСКИМИ ЗДАНИЯМИ?
Из различных построек, которые составляют дети, мы ограничимся правилами:
- все кубики одинакового размера;
- соединять кубики нужно, так, чтобы одна стенка прилегала полностью к другой всей площадью;
- вертикальные башенки (или подъезды) в кубическом здании можно перенести на другое место одной рукой;
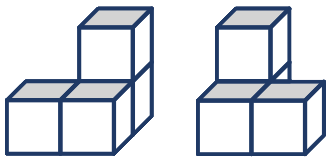
Таким образом, постройка на рисунке (рис.1) в нашем смысле не является кубическим зданием, так как нижняя стенка жёлтого кубика перекрывает верхнюю стенку фиолетового и оранжевого кубиков лишь частично.
Рис.1
Когда дети только начинают знакомиться с этим дидактическим блоком КУБИЧЕСКИЕ ЗДАНИЯ, необходимо дать им время, чтобы «наиграться». Только после этого вводить игровые ограничения
В детском саду
Сначала дети строят постройки в соответствии со своим воображением: стены, дома, ручки, лестницы, башни…
Опыт рук помогает развить пространственное воображение ребёнка. Взрослый может помочь ребенку тем, что проявляя интерес к постройкам, в общении будет комментировать его слова.
Ребенок говорит про угол кубика, а мы, не исправляя ребенка, называем его «вершина». Ребёнок скажет: «вот я положу это на это». Мы можем прокомментировать его деятельность: «я вижу, что ты прикрепил стену к стене.» Уже сейчас так же развиваются аргументационные способности детей. Язык, который ребёнок использует для описания постройки, отражает его собственный опыт и представления, таким образом, ребёнок объясняет и использует свои названия и объясняет себе описания других детей. Ребёнок развивает свои коммуникативные навыки ради общения.
После того, как дети делали постройки по своему вкусу и фантазии, можно начать ограничения с того, что предложить им строить только так, чтобы одна стенка кубика полностью соприкасалась со стенкой другого кубика. Потом от свободного творения переходить к копированию. Дети с удовольствием и спонтанно копируют постройку товарища. Часто между детьми происходит сотрудничество и обсуждение того, куда положить кубики. Видно, что взгляд ребенка на здание уже более глубокий, он замечает детали, например, количество кубов, их расположение, количество этажей и т. д. Здесь начинают появляться будущие понятия, такие как объем, высота тела, поверхность, …
Игра в прятки развивает кратковременную пространственную память и готовит будущих понятие общности предметов. Собрать в укромном месте КУБИЧЕСКОЕ ЗДАНИЕ. Ребенок находит её, запоминает и ставит у себя на ковре или парте. Затем скрытое здание «приходит посмотреть» для проверки.
Это задание интересно выполнять и в работе малыми группами. И проверку делать, сначала сравнивая как получилось у других, а потом уже своё. Или сначала команды проверяют здания соседней команды, а потом своё. Это называется ВЗАИМНАЯ ПРОВЕРКА.
Реакция детей при сравнении зданий, будь то одинаковых, или в зеркальном отражении, или в противном случае видоизменённых, как правило, спонтанное, радостное и сопровождается дискуссиями.
1. и 2. классы
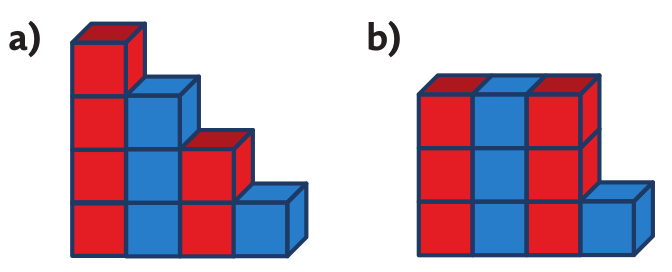
Задача 1: Постройку на рисунке (а) назовем 4-ступенчатая лестница. Постройте её. Сколько кубиков понадобится для этой постройки? Каких кубиков больше красных или синих?
Многие дети считают по одному. Появляются и решения, 1 + 2 + 3 + 4 = 10, или: синие 1 + 3 и красные 2 + 4, итого 10. У ребёнка, которого предупреждают, что там могут быть спрятанные кубики, которые не видны на картинке, развивается геометрическое мышление — способность работать с объектами в уме, которые в данный момент не воспринимаются зрением. Дети также получают опыт работы с нечётными (синими) и чётными (красными) числами, а так же с ритмом.
Вопрос: «каких кубиков больше на лестнице?»одна девочка решила, переместив самый верхний красный куб так, как на рисунке (b).
Не считая, она ответила, что красных кубиков на 2 больше. Мы видим, что пространство удивительно велико для разных аргументов детей.
Еще одна задача — поддержать восприятие ритма и последовательности чисел
Задача 2: Добавьте одну башню и создайте 5-уровневую (6-уровневую, 7-уровневую) лестницу. Как может ребёнок поступить, когда перед ним такая задача? Некоторые дети следуют ритму цветов и строят башню из пяти синих кубов, а затем отвечают, некоторые дети объясняют прежде чем строить, некоторые вообще не строят и решают задачу только в воображении.
Следующая задача развивает комбинаторное мышление.
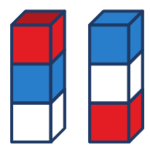
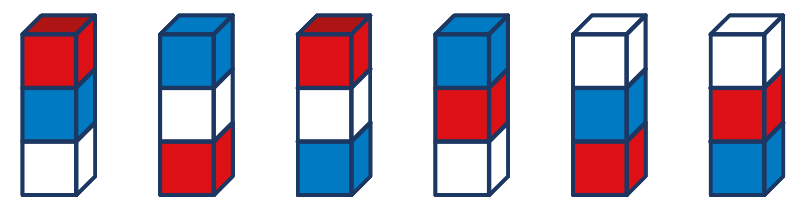
Задание 3: На рисунке показаны две разные башни из трёх кубов — красного, синего и белого. Сколько разных башен вы можете построить из этих трёх кубов?
Задача 4: Жители планеты Куб живут в кубических зданиях. Каждое здание построено из четырёх кубов. Какое максимальное количество зданий может получиться, если ни одно из зданий не будет повторяться?
Задача связывает геометрию и комбинаторику и в случае отсутствия кубов вызывает необходимость в какой-то записи. Обычно дети обсуждают, какие здания одинаковы (идентичны) или являются ли, например, две структуры на картинке одинаковыми или разными. Уля утверждает, что они одинаковые, потому что, когда одна из них смотрит в зеркало, она видит себя так, как будто это она. Гоша против. Он говорит, что левый ботинок отличается от правого. Решение нужно оставить за детьми. Не стоит «спойлерить» в обучении. Иногда на следующем уровне они приходят к пониманию косвенно-идентичным телам.
Постепенно дети начинают записывать планы своих проектов кубических зданий. Целью является развитие и умение понимать записи и уметь создавать план построек. Со временем появляется запись, приемлемая для всех.
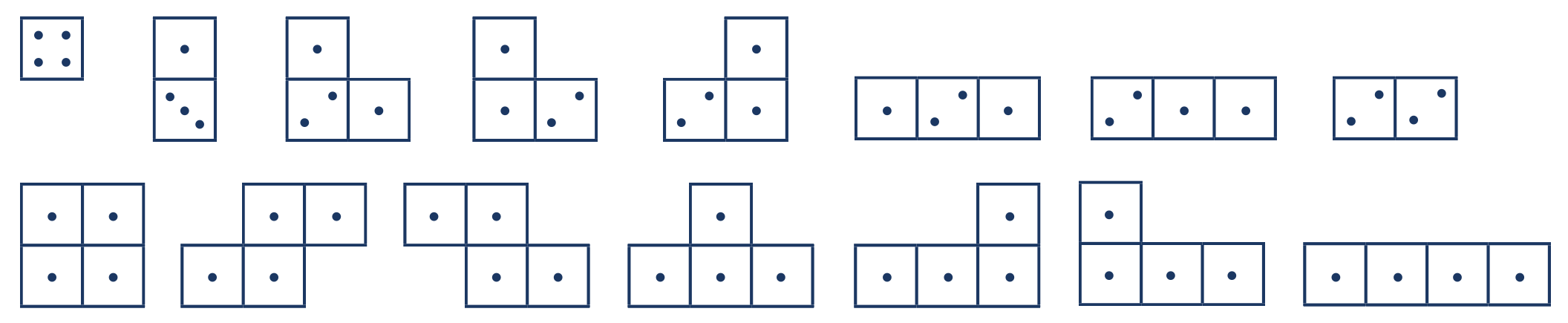
Запишем план здания так: рисуем, как видим его сверху, а количеством точек в одном квадрате выразим количество кубиков (этажей) друг над другом. Так мы получаем план кубического строительства.
На рисунке показан чертеж левой конструкции из рисунка для задания 4.
ОТВЕТЫ:
Задача 3: Всего разных башен из данных трёх кубиков получается 6.
Задача 4: На планете Куб может быть не более 15 различных зданий. (без учёта одинаковых построек, но повёрнутых по разному)
3. и 4. классы
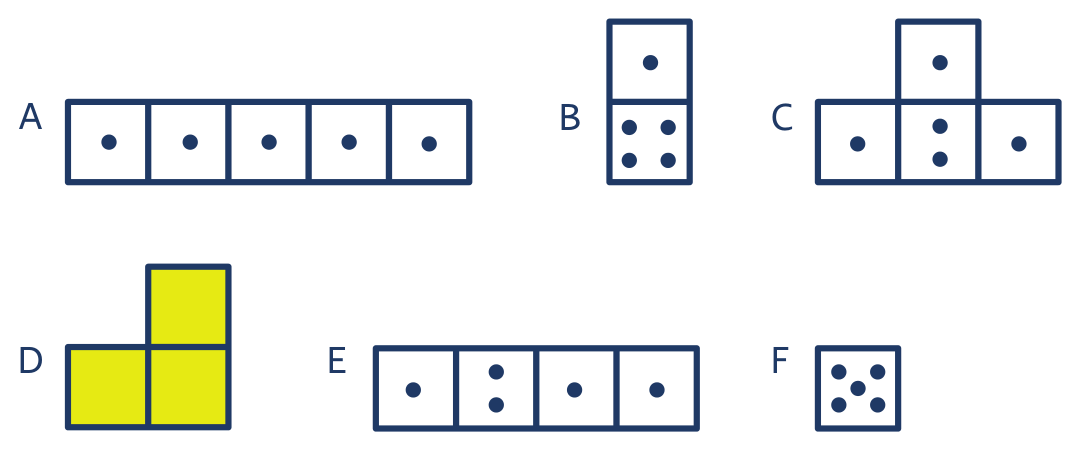
Задача 5: Галина построила из кубиков „поезд » (рис. а). Она переставила один куб в другое место и записала новый проект здания в план. Затем она переставила ещё один кубик и снова записала созданное здание в план. Она повторила это ещё три раза. Наконец, перед ней стояла башня (рис. F). Планы зданий Галина записала на рисунках A, B, C, D, E, F, но в другом порядке. Кроме того, из плана D стёрлись точки. Найдите последовательность планов и добавьте точки в план D.
ОТВЕТ:
4. и 5. классы
Мы работаем с объёмом кубических зданий и осматриваем поверхность. Единица объема — 1 куб, единица записи в плане — 1 квадрат, который является стенкой куба. Например, 4-ступенчатая лестница из Задачи 1 имеет объём 10 кубов и поверхность 36 квадратов.
Задача 6: Какая самая большая и самая маленькая поверхность кубической структуры с объемом:
(а) 4 куба
(б) 8 кубов
в) 27 кубов
ОТВЕТ:
Задача 6: Представьте, как создается здание, добавив один куб. Поверхность будет наилучшей, если мы «склеим» каждый добавленный куб только одной стеной с тем, что уже построено. Можно создать много разных конструкций, проще всего представить себе «башню»
а) 4 × 1 × 1
б) 8 × 1 × 1
в) 27 × 1 × 1
Их поверхность состоит из
а) 18
б) 36
в) 110
Наименьшая поверхность имеет:
а) призма 2 × 2 × 1
б) куб 2 × 2 × 2
в) куб 3 × 3 × 3
Их поверхность состоит из
а) 16 квадратов
б) 24 квадратов
в) 54 квадратов
Терминология приходит естественным путём, определения и правила дети сами составляют. Не УЧИТЬ! Не ОБЪЯСНЯТЬ!

Опубликовано: 09.04.2020
Кубические здания. Приём из методики Хейни. Математика интересна и любима детьми, если им дают возможность самим её для себя открывать.

Опубликовано: 25.01.2020
Дети не ждут, пока результат появится на доске. Они работают в группах, парами или даже самостоятельно. Таким образом, каждый учащийся может рассказать, как он / она пришёл к результату, и объяснить его другим. Результат рождается на основе совместной работы. Преподаватель не является здесь абсолютным авторитетом, чтобы просто сказать, где истина, — и переворачивает следующий лист учебника. Ученики строят свои собственные полноценные знания, о которых они постоянно думают.

Опубликовано: 25.01.2020
Учебники методики Хейни содержат задания всех уровней сложности. Поскольку слабые ученики всегда решают некоторые задачи, это предотвращают чувство тревоги и ужаса на следующих уроках математики. В то же время перед сильными учениками постоянно ставятся дополнительные проблемы, чтобы они не скучали. Учитель не перегружает задания, но задаёт так, чтобы постоянно мотивировать детей. Он делит задачи в классе в соответствии с потребностями ребенка.

Опубликовано: 25.01.2020
Ребенок, которому запрещено падать, никогда не научится ходить. Анализ ошибок приводит к более глубокому опыту, благодаря которому дети могут лучше запомнить свои знания. Ошибки используются как средство обучения. Мы поощряем детей самим находить ошибки и учим их объяснять, почему они допустили ошибку. Взаимное доверие между ребёнком и учителем способствует радости учеников от проделанной работы.

Опубликовано: 25.01.2020
Привычная социальная идея учителя — это образ человека, который знает, умеет и учит. Таким образом, учитель математики знает математику, поэтому он может о ней говорить. Во многих случаях это так и делается. Ребёнок слышит интерпретацию учителя, записывает некоторые заметки в рабочую тетрадь, слушает объяснение учителя, а потом учится использовать. В нашем понимании преподавания математики, роль учителя и ребенка совершенно иная.

Опубликовано: 25.01.2020
Когда первоклассник строит квадрат из деревянных брусков, он берет один брусок, затем второй, третий… Ему всё еще не хватает, поэтому он берет четвертый брусок и получается квадрат. Затем он решает надстроить квадрат по высоте. Тогда он берет несколько брусков и надстраивает квадрат. Он уже начинает догадываться, что если он хочет построить ещё один ряд квадрата, то ему всегда нужно взять ещё четыре бруска. Так он встаёт на путь к открытию формулы для расчета периметра квадрата.

Опубликовано: 25.01.2020
По опыту ясно: самая эффективная мотивация исходит от чувства успеха ребенка, от его искренней радости, от того, насколько хорошо он решил достаточно сложную задачу. Это радость собственного прогресса и признательность одноклассников и учителей. Детям незнакомы «математические блоки», о которых уже ходят легенды в чешской системе образования. Но, когда они видят формулу, их реакция — не отвращение, а энтузиазм: «я знаю, что я это решу!»

Опубликовано: 25.01.2020
Мы используем собственный опыт ребенка, который он накопил с самого первого дня своей жизни — дома, с родителями, при изучении мира вне дома или в песочнице с другими детьми. Мы опираемся на естественный конкретный опыт, из которого ребенок может затем сделать общий вывод. Например, дети «шьют одежду» для куба, автоматически узнавая, сколько стенок у куба, сколько вершин, как рассчитать его поверхность…

Опубликовано: 25.01.2020
Все математические задачи в методике Хейни построены таким образом, что их решение автоматически «развлекает» детей. Правильная мотивация — внутренняя, а не навязанная извне. Дети приходят к решению задач своими силами. Мы не крадем у детей радость собственного успеха. Благодаря коллегиальной атмосфере в классе аплодисменты получают все — даже те, кто приходит к пониманию или решению позже.

Опубликовано: 25.01.2020
Одним из главных мотивов профессора Хейни в создании новой методики был акцент на том, чтобы дети не манипулировали в своей жизни. Поэтому учитель при обучении не передает готовые знания, а учит детей в первую очередь спорить, обсуждать и оценивать. Тогда дети сами знают, что для них правильно, уважают другого и умеют принимать решения. Они отважно несут последствия своих действий. В дополнение к математике они, естественно, также открывают основы социального поведения и морально развиваются.

Опубликовано: 07.01.2020
Автобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

Опубликовано: 06.01.2020
Автобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

Опубликовано: 02.01.2020
Мы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Мы проходили это две недели назад, мы этого уже не помним…»
Опубликовано: 02.01.2020
Методика Хейни основана на соблюдении 12 основных принципов, которые гениально сложены в целостную концепцию так, чтобы дети открывали математику сами с удовольствием. Методика основывается на 40-летних экспериментах и практически использует исторические знания, которые появлялись в истории математики с Древнего Египта и до наших дней.
Опубликовано: 02.01.2020
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика для дошкольников, учеников начальных, средних и старших классов общеобразовательных школ
Опубликовано: 02.01.2020
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни) — учебные задания для обучения математики в начальных классах по методике чешского математика Хейни

Опубликовано: 17.12.2019
Дидактические блоки способствуют получению неформальных знаний. 2 Принцип методики обучения математики в начальных классах. Никакого страха перед математикой. Дети, выполняя задания сами не замечают, что они работают, для них это интересная игра.

Опубликовано: 15.12.2019
Чешская методика обучения математике детей в начальной школе. Основана на создание рабочей среды на образах и схемах детей. Методика Хейни

Опубликовано: 12.12.2019
Методика Хейни. Игровая образно-наглядная чешская методика по обучению математике в начальных классах.