Третий принцип методики Хейни
Двенадцать принципов методики Хейни
Милан Хейни (Milan Hejný) — Чешский и Словацкий математик
-
- ПОСТРОЕНИЕ СХЕМ: ребенок знает даже и то, чему мы его не учили
- РАБОТА С ДИДАКТИЧЕСКИМИ БЛОКАМИ: обучение при повторных визитах
- ПЕРЕПЛЕТЕНИЕ ТЕМ: математические законы не изолируются друг от друга
- ПЕРСОНАЛЬНОЕ РАЗВИТИЕ: поощрение самостоятельного мышления детей
- РЕАЛЬНАЯ МОТИВАЦИЯ: когда «я не знаю» и «я хочу знать»
- РЕАЛЬНЫЙ ОПЫТ: обучение на собственном опыте ребёнка
- РАДОСТЬ ОТ МАТЕМАТИКИ: серьёзно помогает в дальнейшем обучении
- СОБСТВЕННЫЕ ОТКРЫТИЯ: вес собственных открытий больше, чем чужих
- РОЛЬ УЧИТЕЛЯ: проводник и ведущий обсуждений
- РАБОТА С ОШИБКОЙ: предотвращение ненужного страха у детей
- АДЕКВАТНАЯ СЛОЖНОСТЬ: для каждого ребенка отдельно в зависимости от его уровня
автор: Милан ХЕЙНИ
перевод с чешского: Светлана ФРИГА
Третий ПРИНЦИП. Переплетение тем: математические законы не изолируются друг от друга
Информация не передаётся детям отдельно, она всегда хранится в знакомой схеме, которую ребёнок может вспомнить в любое время. Мы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Наталья Ивановна, мы проходили это две недели назад, мы этого уже не помним…»
Когда мы соотносим отдельные темы в контексте, который соответствует нашему собственному опыту, нам легче вывести и вспомнить знания в любое время. И наоборот, если мы узнаем отдельные факты или правила в изоляции без реального понимания, мы не сможем вспомнить их с течением времени.
Когда информация логически связана
Если бы схему нашей квартиры мы учили так, что в сентябре мы обсудим окна, в октябре кухня, в ноябре ковры и в декабре освещения, то в январе мы должны будем повторить всё, что мы уже об окнах, кухне и коврах забыли. Но поскольку мы узнаем нашу квартиру непосредственно в действии, в повседневной деятельности, которая сочетается и переплетается по-разному, мы можем вспомнить всю квартиру и её части в любое время.
Происходят процессы при которых мы действуем. Действия естественно переплетаются в различных областях нашей квартиры, связывая несколько подсхем. Например вывешивание картин в гостиной — это занятие, которое переплетается со схемами гостиной и окон. Перед тем, как повесить картины, мы рассмотрим, где их будет освещать дневной свет, затем искусственное освещение, а также то, как картинка будет гармонировать с другими украшениями в гостиной и т.д. Мы хорошо знаем нашу квартиру, её отдельные области, хотя мы никогда не учили их. Вся эта информация хранится в диаграмме квартиры, и мы почти всегда можем её запомнить, хотя это может занять некоторое время.
Различные схемы облегчают понимание
Нечто подобное происходит и в методике Хейни. В различных средах или задачах мы определяем отдельные концепции, процессы, стратегии решения, явления, отношения, и их хорошее понимание происходит путем объединения частей мозаики частичных знаний из отдельных дидактических блоков и из различных видов деятельности.
Вот два примера. В первом из них мы покажем, как один вид деятельности смешивается во многих областях. Во втором мы опишем, сколько разных видов деятельности способствуют созданию одного знания.
1. СКЛАДЫВАНИЕ ЛИСТА БУМАГИ
В очень простом упражнении, например, сворачивании квадратного листа бумаги в два одинаковых треугольника, дети используют свой опыт для создания:
- геометрические понятия — квадрат, треугольник, прямоугольный равнобедренный треугольник, диагональ квадрата, вершина и сторона квадрата и треугольника, гипотенуза прямоугольного треугольника, содержание (квадрат может состоять из двух треугольников);
- геометрические отношения — тождество треугольников, квадрат можно разделить на два равнобедренных прямоугольника и наоборот, тождество сторон квадрата и треугольника, диагональ квадрата длиннее его стороны;
- арифметические термины — число 2, т.е. два треугольника; дробь как часть целого, то есть половина квадрата.
Обращаясь и пытаясь сложить бумагу, дети также развивают мелкую моторику, которая позже будет использована при конструировании. Это основная идея задач, предлагаемых детям в разных средах — решая задачи, ребенок не только проявляет свои расчетные навыки, но и распознает что-то иное, нежели фокус задачи. Каждая среда приносит что-то конкретное в математику.
Дети также развивают мелкую моторику при манипулировании и попытке сложить бумагу как можно точнее, это будет использоваться позже в проектных задачах. Это существенная идея задач, предлагаемых детям в разных заданиях – решая задачи, ребёнок не только тренирует свои математические навыки, но познает … и что-то другое, чем то на что работа непосредственно направлена. Каждый дидактический блок привносит что-то особенное в изучение математики.
2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В РАЗЛИЧНЫХ ДИДАКТИЧЕСКИХ БЛОКАХ
Во втором примере давайте посмотрим на сложение и вычитание, и как ребенок может идентифицировать эти простые операции везде:
- при играх и работе с блоком ШАГИ и ЛЕСТНИЦА (шагание, хлопанье в ладоши, повторение чисел, шагание по стрелкам);
- при игре и решении задач по дидактическому блоку АВТОБУС (пассажиры садятся в автобус и выходят из него); (видео)
- работа с ЖИВОТНЫМИ ДЕДУШКИ ЛЕСОНА (создание команд равной силы);
- в ПАУТИНЕ и многих других блоках, где уже играют роль только числа (структурные блоки);
- в геометрических блоках, которые не сосредоточены на арифметических операциях, таких как ПАРКЕТ (выбор паркета, необходимого для покрытия данного пола), ДЕРЕВЯННЫЕ ПАЛОЧКИ (взять три палочки, чтобы сформировать треугольник, взять еще два и создать два треугольника), кубические здания (построить конструкцию так, чтобы было три куба на первом этаже и два на втором этаже) и т. д.
Каждый из этих дидактических блоков по-своему способствует пониманию концепции числа и простых операций сложения и вычитания. Более того, это создает условия для различных стратегий решения.
Примеры дидактических блоков:
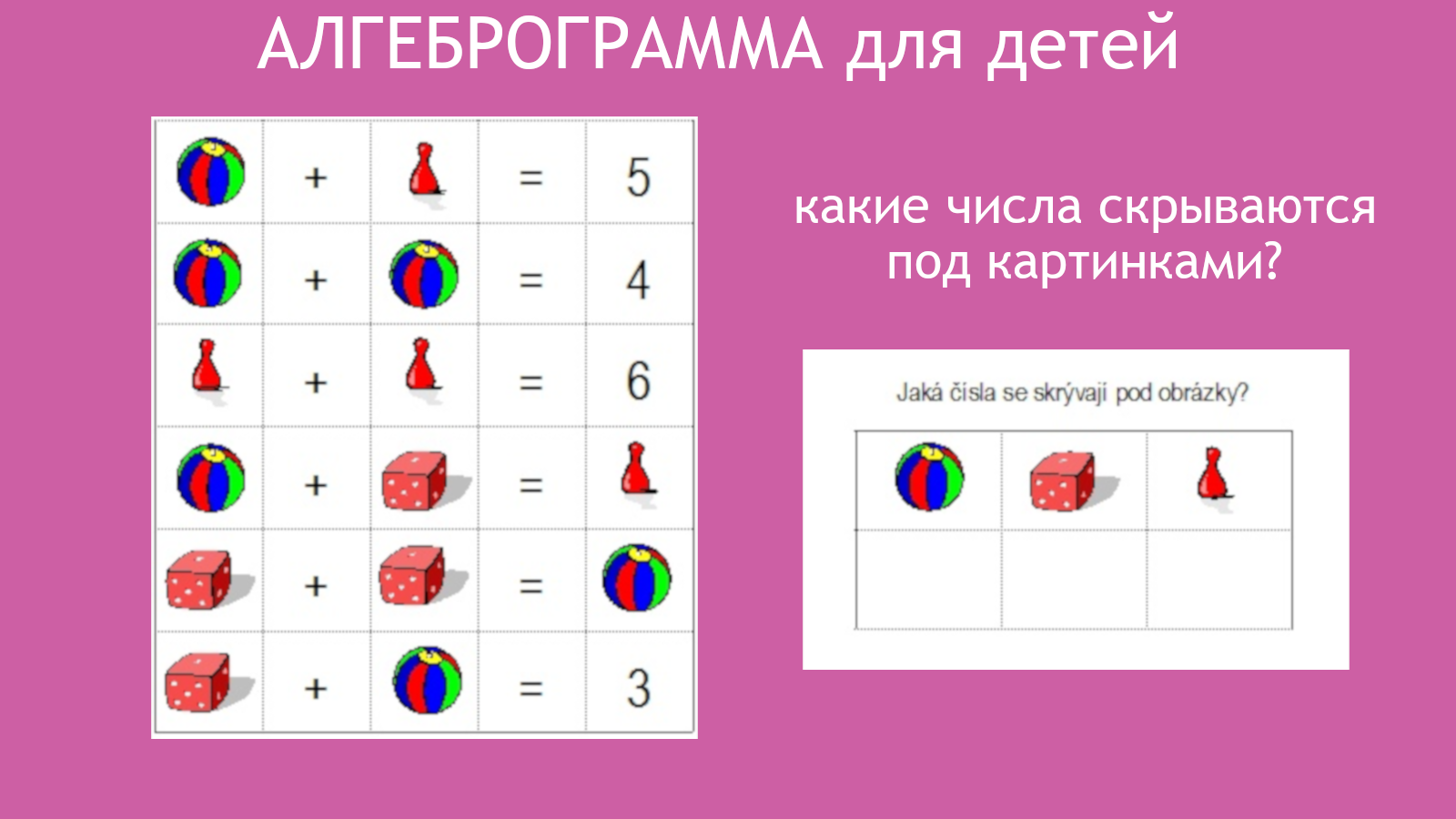
алгеброграммы
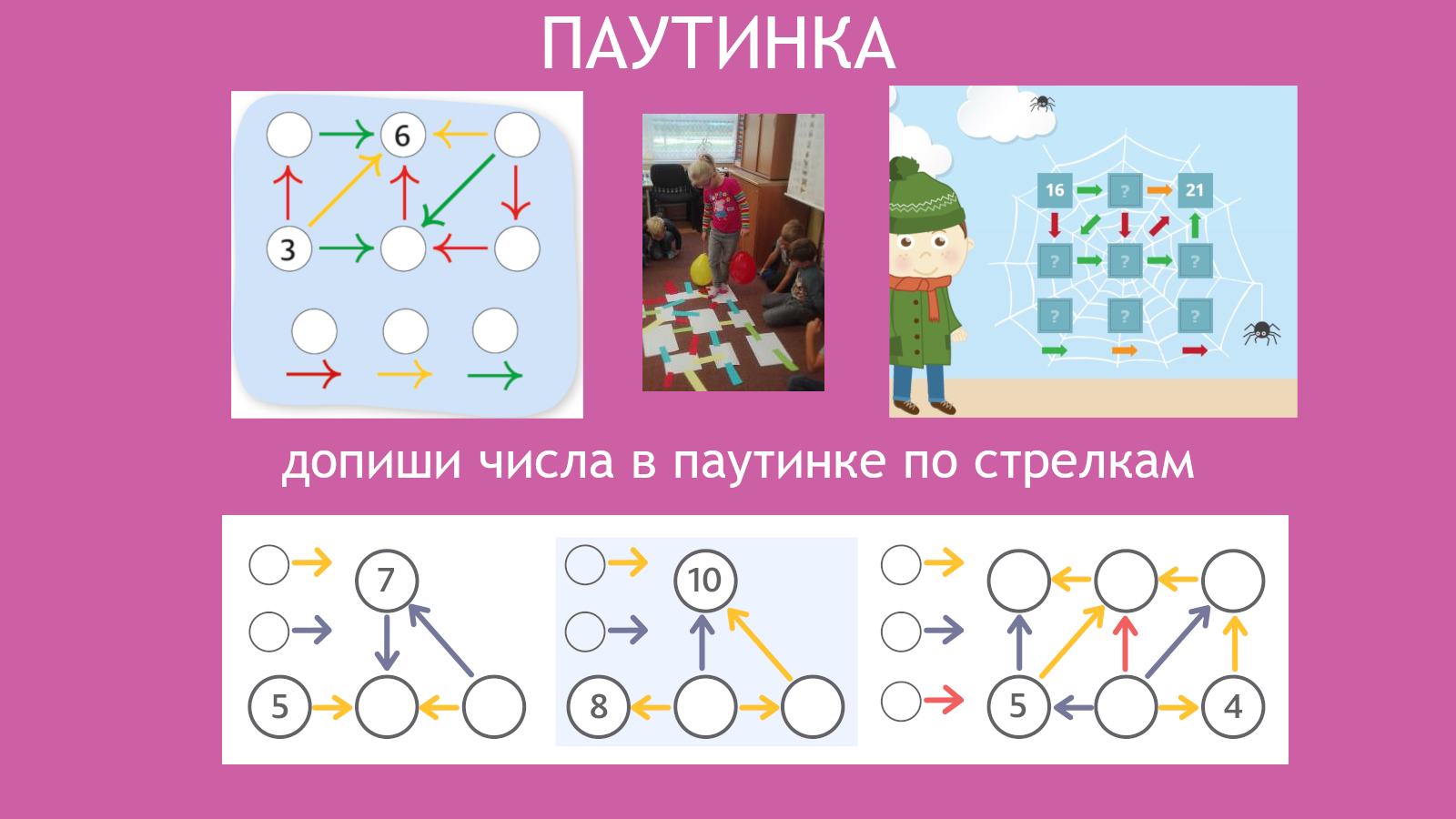
паутинка
змейки
суммарные треугольники
квадраты умножения
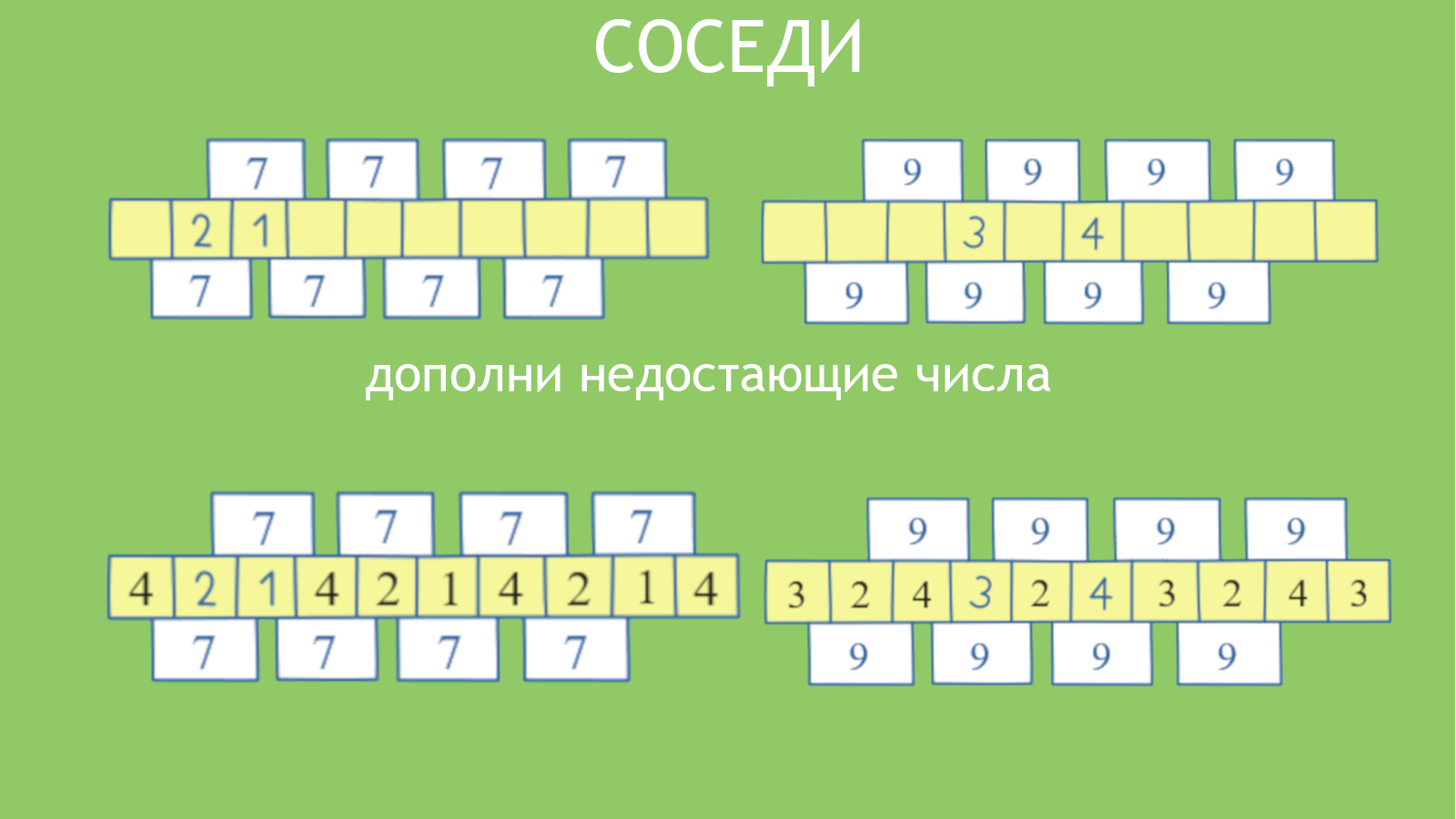
соседи
зверушки лешего
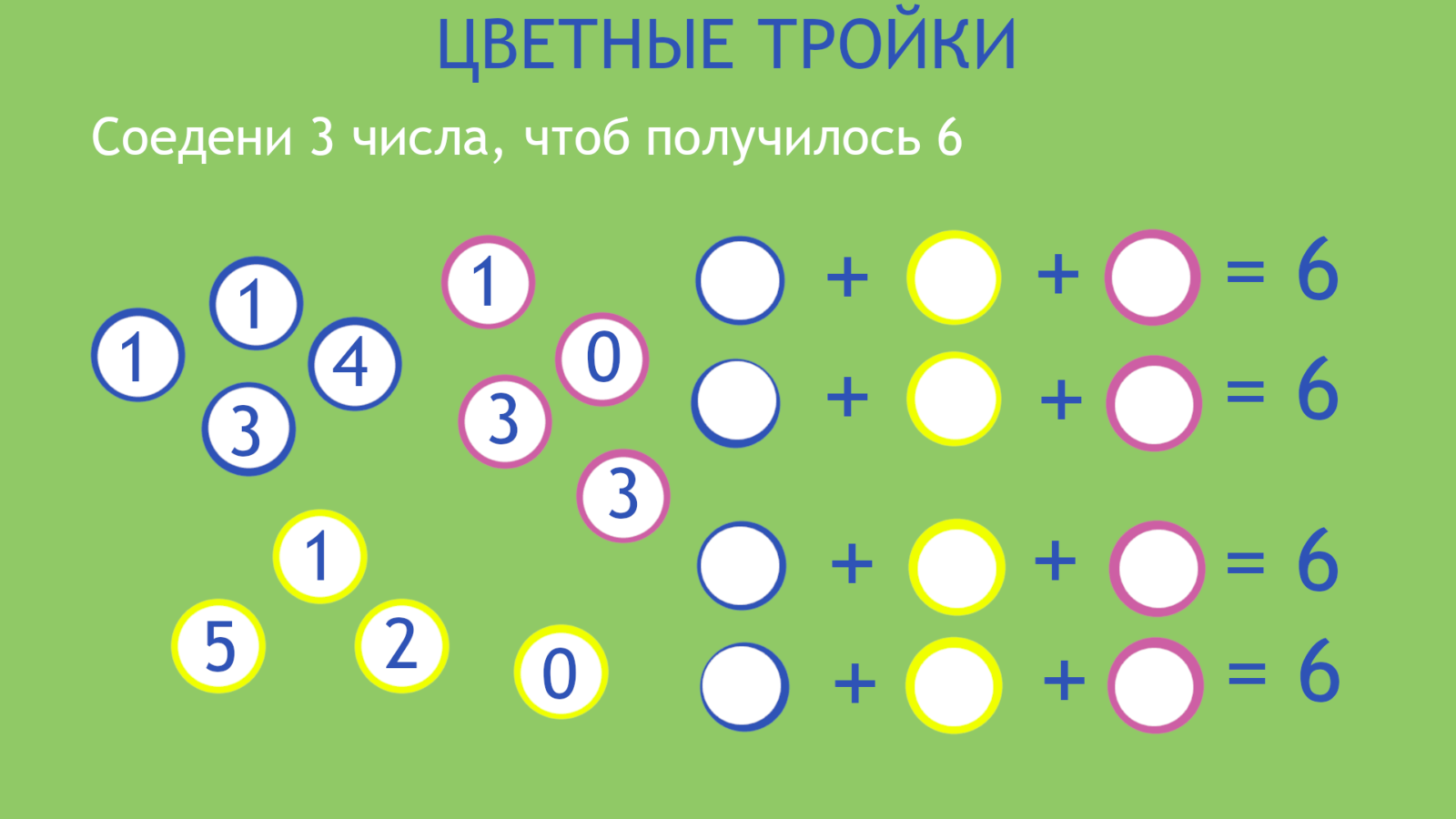
цветная тройка или непоседа
План организации и проведения Театра теней. Занятие с детьми 3-6 лет в детском саду
Театр теней с детьми в детском саду
(методическое пособие для занятий с дошкольниками)
\формат для скачивания: PDF
объем: 14 страниц
тема №1: Интеграция двигательно-коммуникативного стиля обучения в онлайн среду начальной школы (приёмы, обоснование, технические возможности) для школьного и семейного обучения
Когда все эти подготовительные действия делаются регулярно, на них уходит очень мало времени, но они создают настрой и благоприятную среду.
Дружное эхо
Дружное эхо можно использовать в разных моментах урока. Универсальная игровая разминка. Для незнакомых групп, большой и малой аудитории. Легко проводить.
Тише едешь — дальше будешь (ЗАМРИ!)
Узнайте о традиционной детской игре «Тише едешь — дальше будешь» и ее применении в педагогике. Эта игра развивает внимание, координацию и дисциплину у школьников, помогая им учиться молниеносно реагировать на команды и творчески оправдывать свои действия. Идеальная разминка для класса, которая способствует командной работе и индивидуальному развитию.
