В.М.Букатов, доктор педагогических наук, профессор МПСУ,
научный руководитель экспериментальных площадок
по социо-игровой педагогике:
О ТАБЛИЦЕ-БАБОЧКЕ СОЦИО-ИГРОВОГО СТИЛЯ ОБУЧЕНИЯ И ДРАМОГЕРМЕНЕВТИЧЕСКОЙ ПОВСЕДНЕВНОСТИ НА ШКОЛЬНЫХ УРОКАХ
Перечень статей, поясняющих драмогерменевтическую таблицу-БАБОЧКУ
- Наглядная система профессиональных подсказок, адресованных интуиции учителя открыть в новом окне
- Три социо-игровых постулата педагогического мастерства открыть в новом окне
- О герменевтических подходах к пониманию открыть в новом окне
- Групповая коммуникативность как один из секретов успешности обучения открыть в новом окне
- Процедурная драматургия герменевтической «цепочки понимания» открыть в новом окне
- Прокрустово ложе творческого самовыражения открыть в новом окне
- О профессиональных подоплёках табличных построений открыть в новом окне
- Соблюдение последовательности как показатель профессионализма открыть в новом окне
5. Процедурная драматургия герменевтической «цепочки понимания»
5.1. Эффективная объемность табличных сопряжений
5.2. Оглашенное удивление
5.3. Подсказки от Тютчева
5.4. О смене мизансцен на уроке
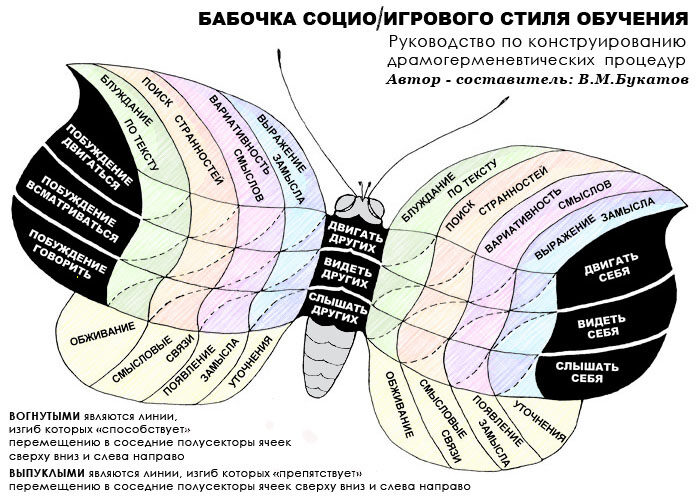
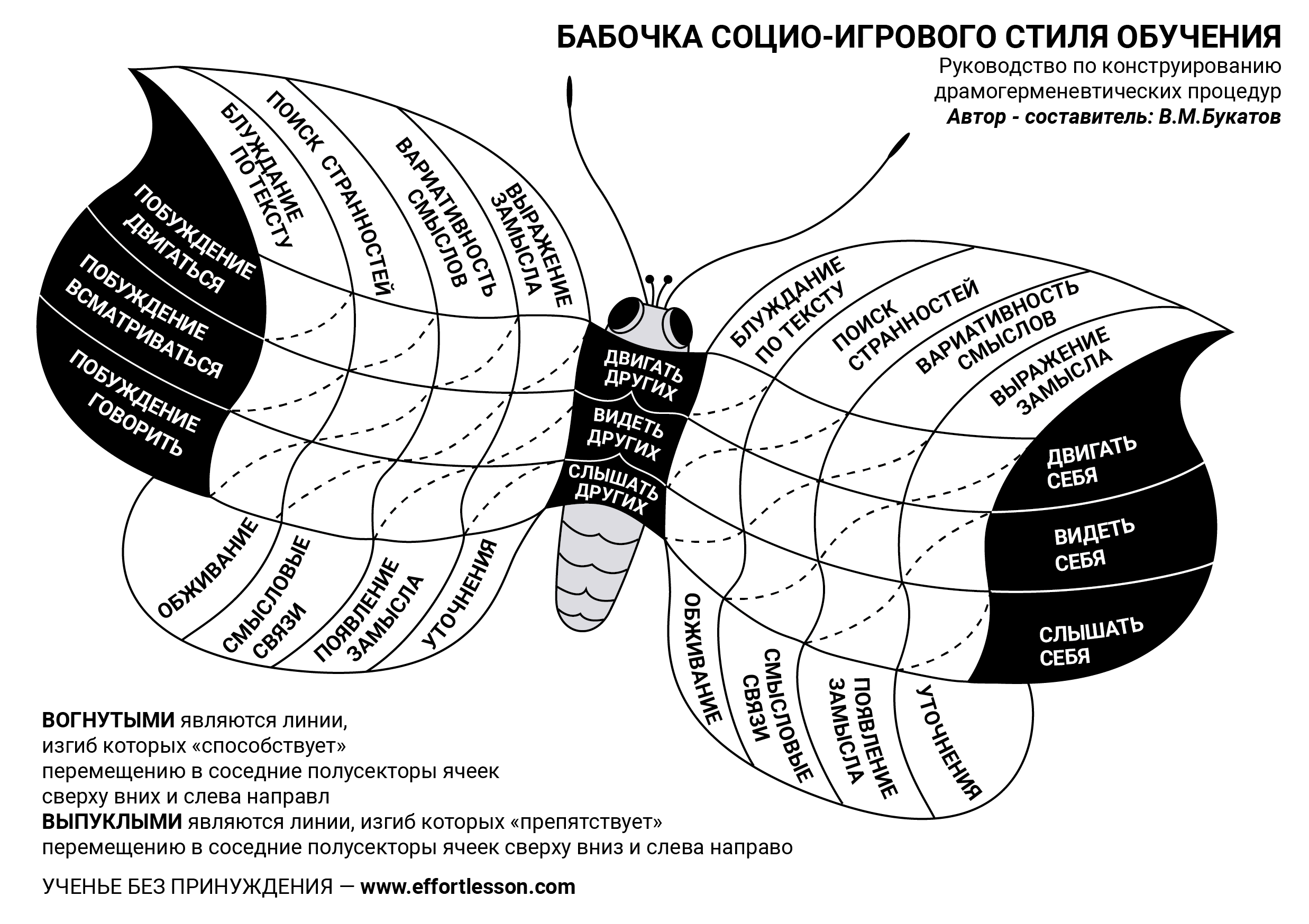
В социо-игровой герменевтике существует так называемая процедурная цепочка неких взаимосвязанных приемов, приводящих к личностному пониманию сложного, непривычного, пугающего своей новизной текста. На БАБОЧКЕ эта цепочка воспроизведена дважды: на правом крылышке и на левом.
Напомним, что верхние и нижние колонтитулы содержат герменевтическую маркировку. Расположенные друг над другом ячейки верхнего и нижнего колонтитулов как бы образуют обособленные звенья, которые своим следованием друг за другом близки к образу цепочки. И каждое звено-столбец этой цепочки имеет свое начало (в верхнем колонтитуле) и свое завершение (в нижнем колонтитуле).
В верхнем колонтитуле каждого из звеньев приведены ключевые слова, связанные с содержанием организуемой учителем соответствующей герменевтической процедуры (или, что, пожалуй, будет точнее, — определенного «звена герменевтической цепочки»). А в нижних — ключевые слова, указующие на психолого-личностные приобретения, возникающие у учеников к концу данного звена «процедурной цепочки».
5.1. Эффективная объемность табличных сопряжений
Напомним, что ячейки всех четырех столбцов (что находятся между верхними и нижними колонтитулами с герменевтической маркировкой) на каждом крылышке имеют особую — боковую — маркировку. Она связана с сопряжением коммуникативно-деловых побуждений субъекта (то двигаться и руководить, то всматриваться и видеть, то говорить и слышать) с рефлексивной направленностью его сознания (то на других, то на себя).
В результате конкретизации, возникшей «на пересечении» трех параметров-характеристик —
1) герменевтических,
2) коммуникативно-деловых и
3) рефлексивных
— картина будущей деятельности ребенка обретает вполне ощутимые и реальные очертания. Она становится как бы объемной, что делает таблицу-Бабочку (в соответствии с исходной сверхзадачей ее создания) по-настоящему эффективным подспорьем учителям, ломающим голову над тем, как «понестандартнее», поживее и поинтереснее подготовить и (или) провести свой очередной урок.
5.2. Оглашенное удивление
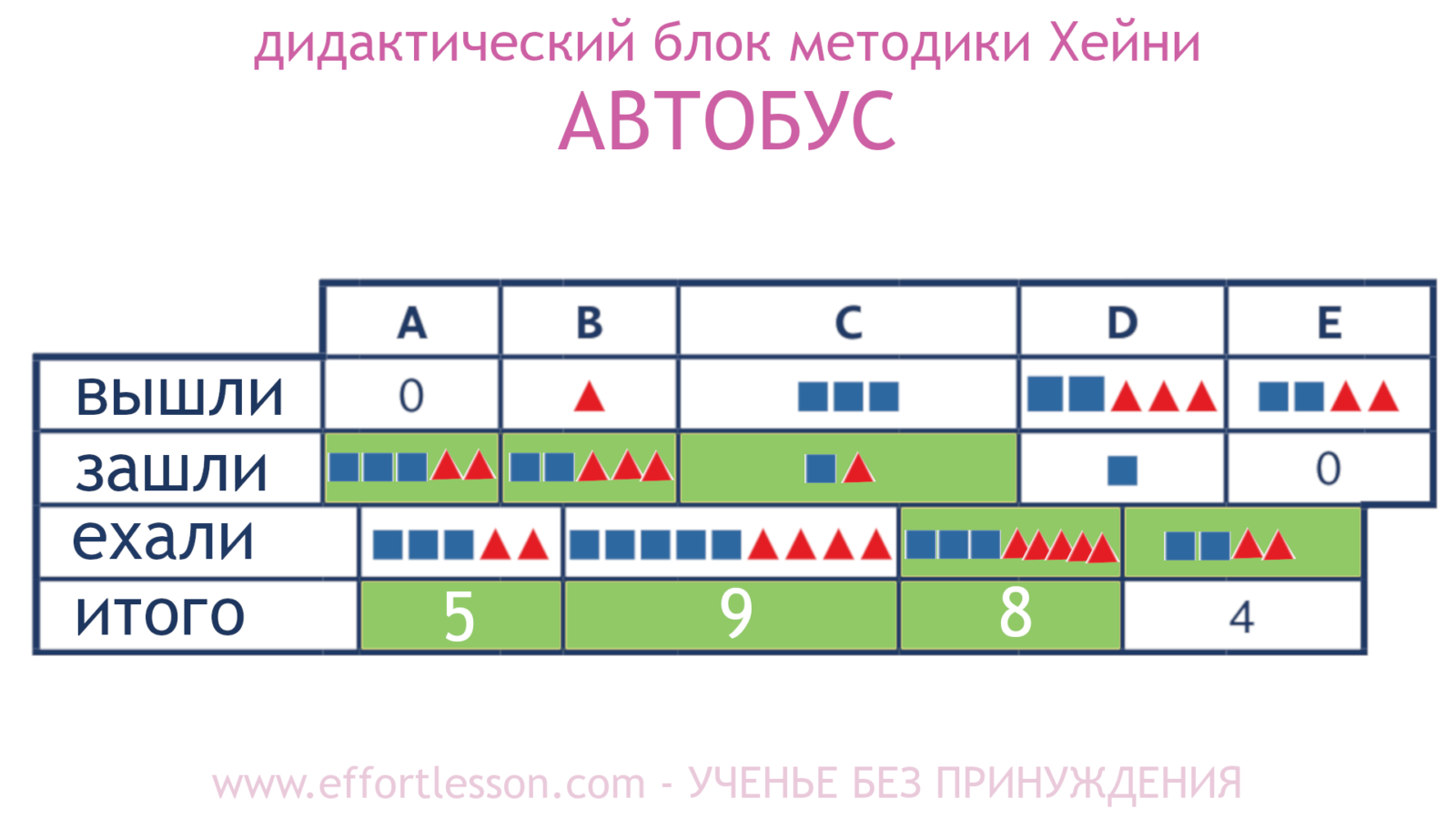
Первое процедурное звено герменевтической цепочки — блуждание по тексту. Когда мы позволяем себе бесцельно ползать по«тексту» (каким бы он ни был — живописным, литературным, математическим и т.д.), то он перестаёт нас пугать своей новизной. Потому что мы начинаем то и дело обнаруживать в нем что-то нам уже известное, близкое и понятное.
(Интересно, что первоначально идея придать таблице образ бабочки возникла именно из этого звена герменевтической цепочки — блуждания по тексту.)
Блуждание по тексту — это универсальное начало для любой герменевтической деятельности. Мы находим его в левой стороне верхних колонтитулов (напомним, что колонтитулы размещены дважды: и на левом, и на правом крылышках). А обживание, обозначенное в нижних колонтитулах тех же столбцов из светлых ячеек-треугольничков, является конечным результатом этого процедурного приема. Если мы этот результат получили — то есть текст перестал пугать читателя своей новизной и даже наоборот начал производить впечатление «доброго знакомого» — можно смело переходить к более сложной процедуре.
Начало второго звена в герменевтической цепочке — поиск странностей. Когда дети вдруг улавливают какие-то странности или нелепости в изучаемом материале, то их учителей и воспитателей это частенько застает врасплох, и они спешат сделать вид, что никаких таких странностей в хрестоматийных текстах нет и быть не может. Но именно с неожиданного обнаружения ребенком каких-то странностей для него и начинается освоение зоны своего ближайшего развития.
Все искусствоведы также согласны, что и художники при создании своего произведения искусства и зрители при восприятии этого произведения без странностей не обходятся. Не случайно Пушкин в своих черновиках помечает, что странности бывают двух родов: первые происходят от недостатка разумения, а вторые — от избытка разумения и недостатка слов, для его выражения.
Ярким тому примером была речь Евгения Евгеньевича Шулешко, выдающегося педагога-психолога, автора оригинальной системы обучения детей письму и чтению. В ходе своих лекций и открытых уроков на мастер-классах он от избытка тонкостей мысли и недостатка слов для их адекватного выражения то и дело переходил на эдакий «птичий» язык. Понятен он был, в основном, только неравнодушным педагогам-последователям. Но вот что удивительно: сами дети всё на тех же открытых уроках его странную речь умудрялись без особых усилий понимать практически с полуслова!..
Так вот, второе процедурное звено герменевтической цепочки вынуждает учителя создавать на своих уроках такие ситуации, чтобы дети не только реально находили всевозможные странности в изучаемом материале, но и смело, с удовольствием объявляли о своих находках, выставляя их на всеобщее обсуждение.
В результате поиска странностей у детей непроизвольно начинают появляться какие-то смысловые связи (что свидетельствует о скором завершении данной процедуры). У каждого смысловые связи будут своими, индивидуальными. Подчеркнем, что подобный психолого-личностный эффект будет возникать в любом возрасте — и у детей в начальных классах, и у подростков в средней школе, и на уроках со старшеклассниками.
Вспоминается, как на занятии с шестилетками я устроил «блуждание» малых групп по репродукциям картины Брейгеля «Охотники на снегу». Дошло дело и до поиска странностей. Спрашиваю у них, видит ли кто на картине какие-нибудь странности?
И тут же посыпались варианты: «Люди странно одеты», или: «У них странная обувь». При этом кто-то тут же начал возражать — дескать, это никакая не странность, потому что они живут не сейчас и в другой стране, а там тогда все так ходили.
То есть, для кого-то из детей некоторые «необычные детали» изображения уже облеклись смысловыми связями и поэтому странностями быть перестали. Это свидетельствовало о том, что они в своем «образовательном путешествии» уже продвинулись в одну из ячеек соседнего столбца, обозначающего следующее процессуальное звено герменевтической цепочки.
5.3. Подсказки от Тютчева
Когда странностей набирается достаточно много (а такое случается практически всегда, ведь для каждого они свои, и вскладчину объем их, как правило, получается внушительным), то «чаша странностей», в конце концов, переполняется. И тогда процесс трансформации этих «странностей» в какие-то «смысловые связи» становится лавинообразным. Возникает цепная реакция взаиморазрешения странностей.
Теперь на месте прежних странностей появляются разные версии их смыслового взаиморазрешения — одна другой лаконичнее и/или правдоподобнее. Специально отметим, что, при сравнении их со смысловыми вариантами предыдущих восприятий текста, все они оказываются «новыми». И новизна эта связывается уже не столько с «буквой текста», сколько со смыслом так называемого подтекста, то есть с нашими субъективными предположениями, что же автор своим произведением хотел нам сказать…
Возникновение нового — как бы добавочного — смысла «из ничего» (точнее, из того, что поначалу воспринималось как некие странности и/или нагромождение каких-то бессмыслиц) — принципиальный момент в герменевтической процедурности. И так как новый и/или добавочный смысл у каждого из учеников — свой собственный, то третье процедурное звено герменевтической цепочки — вариативность смыслов — связано, с одной стороны, со сбором, накоплением и перечислением тех смыслов, которые возникли и продолжают возникать в головах учащихся. А с другой стороны, со сравнением, отбраковкой и корректированием этих собираемых смыслов.
Заметим, что наша культура, вопреки кажущейся однозначности и воспроизводимой стабильности составляющих ее смыслов, пронизана малоприметными парадоксами, которые то и дело трансформируются в некие новые, дополнительные смыслы. Тютчев в свое время справедливо подметил:
Нам не дано предугадать, как слово наше отзовётся…
Действительно, учитель может вкладывать один смысл в произносимое слово, а ученик станет понимать его как-то иначе, по-своему. Хотя в конце концов некоторое необъяснимое взаимопонимание, почему-то устанавливается…
И нам сочувствие даётся, как нам даётся благодать.
Таблица-БАБОЧКА была создана как своеобразный маячок, напоминающий учителям, что если они и затевают те или иные изменения в своей привычной режиссуре урока, то рассчитывать им следует не больше, чем на подобное сочувствие (всего лишь!)…
В Хрестоматии игровых приемов обучения (В.М.Букатов, А.П.Ершова; М.,2000 и М.,2002) собраны приемы, с помощью которых учитель может так или иначе «закрутить» обучающую ситуацию на своем уроке. Смысл же подобных социо-игровых инициатив в том, чтобы, у всех присутствующих вместо, например, зависти, презрения или равнодушия, возникало бы всех объединяющее, подлинное и вполне деловое со-чувствие. И в учениках — к окружающим их соседям, и в учителе — к каждому из его учеников.
5.4. О смене мизансцен на уроке
Почему на традиционных занятиях ученическое сочувствие у детей само по себе обычно не возникает? Как правило потому, что мешают мизансцены. Если на занятии нет сочувствия, то мы должны начать менять «рабочие мизансцены». То есть, прямо на уроке начать экспериментировать с размещением своих учеников. Точнее — с расположением малых групп, ученических команд, рабочих компаний.
Перебирая и примеряя всевозможные варианты (в буквальном смысле слова! — то есть, давая всему классу возможность на себе проверить комфортность предлагаемых детьми размещений), учителю нужно «здесь-и-сейчас» искать те позиции, те места и те расположения, которые окажутся классу удобными для работы. Тогда ученикам начнет открываться нечто интересное, как будто на них что-то снизошло…
Добавим, что за образец поиска новых мизансцен на уроке можно брать работу драматических актеров, которые на своих репетициях то и дело заняты поиском «удобных» мизансцен. Для этого они перемещаются по сцене, и так, и сяк примеряясь в пространстве, пока подходящая мизансцена не будет найдена.
Комфортность мизансценического расположения каждой из рабочих групп в едином пространстве (стены классной комнаты никто не покидает— что для социо-игрового стиля принципиально!) будет особо важна при реализации заключительного звена нашей герменевтической цепочки.
Педагогическая составляющая драмогерменевтики
Нередко учитель искренне желает быть отзывчивым, но не замечает, что инициативу на уроке отдает не вовремя, «дистанцию» во взаимоотношениях не меняет, в демонстрации своих сил несдержан, а в поиске общих интересов (или в следовании им) неустойчив…
Герменевтическая составляющая драмогерменевтики
Когда количество странностей начинает превышать «критическую массу», для субъекта наступает их взаиморазрешение новым смыслом. Странности исчезают, уступая место новому пониманию, более углубленному, детальному, эмоционально обновленному…
Театральная составляющая драмогерменевтики
Во время репетиции актеры в поисках «зерна» роли совершают великое множество попутных действий. Зрители же на спектакле, как и ученики на уроке, живут гораздо пассивнее, так как ограничены в совершении попутных действий…

О трёх составляющих драмогерменевтики
Освоение драмогерменевтики неизбежно связано с накоплением личного педагогического и жизненного опыта. Чем старше педагог, тем более связно могут формироваться его представления о драмогерменевтике
О педагогике, как реально практикующем искусстве
Совершенствование своего собственного поведения освобождает учителя от многих абстрактно-педагогических разговоров о дидактических и воспитательных целях, задачах и методах. Сущность такого освобождения мы и определяем составным термином драмогерменевтика.
Блуждание по картинке
Блуждание по картинке один из социо-игровых приёмов Родной педагогики для углублённого изучения и понимания изображений. В помощь взрослым для обучения детей глубокому и осмысленному пониманию, развитию своего видения. Для изучения новых учебных материалов. Для знакомства и изучения искусства. Для интересных уроков.
8. Соблюдение последовательности как показатель профессионализма
Некоторые дети весьма чутко реагируют даже на малейшие нарушения учителем той естественности, которая присуща самому протеканию многоступенчатого процесса понимания. Поэтому специально для учителей эта естественность зафиксирована в последовательности герменевтических процедур.
7. О профессиональных подоплёках табличных построений
Ученическое продвижение по треугольничкам, как можно сказать и будет являться самым настоящим образовательным путешествием. Оно обычно происходит скачкообразно и непоследовательно. И у каждого ребенка траектория путешествия оказывается индивидуальной.
6. Прокрустово ложе творческого самовыражения
Последнее звено в цепочке процедурных приемов, связанных с пониманием текста, — выражение замысла. Некоторые учителя упорно называют это звено «творческим»
5. Процедурная драматургия герменевтической «цепочки понимания»
В социо-игровой герменевтике существует так называемая процедурная цепочка неких взаимосвязанных приемов, приводящих к личностному пониманию сложного, непривычного, пугающего своей новизной текста. На БАБОЧКЕ эта цепочка воспроизведена дважды: на правом крылышке и на левом.
4. Групповая коммуникативность как один из секретов успешности обучения
Многие школьные методики предлагают учителю какие-то свои особые рецепты того, как ему на уроке обеспечить каждого ученика полноценно-деловой занятостью. Есть такой рецепт и в социо-игровой педагогике: почаще организовывать на своих уроках работу малых групп.
3. О герменевтических подходах к пониманию
Начнем с того, что когда ученик говорит:«А, всё ясно!» — и машет рукой, это вовсе не значит, что он действительно все понял. Равнодушное махание рукой к пониманию не ведет и понимания не обеспечивает.
Наглядная система профессиональных подсказок
В.М.Букатов, доктор педагогических наук, профессор МПСУ, научный руководитель экспериментальных площадок по социо-игровой педагогике: О ТАБЛИЦЕ-БАБОЧКЕ СОЦИО-ИГРОВОГО СТИЛЯ ОБУЧЕНИЯ И ДРАМОГЕРМЕНЕВТИЧЕСКОЙ ПОВСЕДНЕВНОСТИ НА ШКОЛЬНЫХ УРОКАХ 1. Наглядная система профессиональных подсказок, адресованных интуиции учителя: 1.1. Плавные контуры летающей симпатяги 1.2. О вертикальной и горизонтальной маркировке Обращаем особое внимание — системой подсказок, а не очередной методичкой-инструкцией, наподобие тех, […]

Драмогерменевтическая таблица-БАБОЧКА
Наглядная система профессиональных подсказок, адресованных интуиции учителя. Основная задача таблицы-БАБОЧКИ — обеспечить учителей системой наглядных подсказок: какие именно из известных им методических социо-игровых приемов имеет смысл использовать, организовывать и проводить на своих ближайших уроках.
Дидактические перспективы: от социо-игрового стиля обучения к драмогерменевтике
В герменевтике — науке об искусстве понимания — констатируется, что в книгах читатель может найти или пищу для размышления над уже знакомыми и доступными проблемами, или подтверждение правильности своих решений, уже ранее найденных.