Это комплексные действия, направленные на создание инфраструктуры, которая позволила бы обеспечить всеми необходимыми ресурсами общину для реализации целей и задач, а так же взятыми на себя обязательствами. “Сельское сопровождаемое проживание для семей с детьми с ограниченными возможностями” (в том числе с такими диагнозами как: аутизм, синдром Дауна, ДЦП и др.) Столярная мастерская организована при Храме Владимирской иконы Божией Матери для поддержки социального проекта. Мастерская не только зарабатывает средства на сопровождение инвалидов, но и организует им рабочие места, исходя из их индивидуальных возможностей. Задача перед мастерами столярной мастерской обеспечить продукцией заказчиков, для развития и поддержания проектов общины. Создание рабочих мест для людей с особенностями и для молодёжи, в качестве обретения профессии. Сегодня после года напряженной работы и помощи друзей мы открыли новое направление в производстве. Начала работать наша столярная мастерская. Бог в помощь всем участникам этого удивительного дела! Уже несколько лет мы вынашивали идею организации профессиональных мастерских, которые могли бы обеспечивать финансовую помощь нашему «Проекту сопровождаемого проживания» и одновременно могли бы предоставлять рабочие места людям с ограниченными возможностями, которые участвуют в проекте. Есть возможность изготовления керамических изделий. Свадьбы, венчания, крещения в православной и русской традиции. Игры и подростковые и детские украшают жизнь в Давыдово. Кадрили, хороводы, танцы тщательно собираются, разучиваются и используются. В наше бурное время многие оказываются в трудной жизненной ситуации. Некоторым из них требуется пережить штормы житейского моря, чтобы спокойно помолиться, потрудиться, собраться с силами и понять, как жить дальше. Таким людям наша община оказывает посильную помощь.Три цели нашей хозяйственной деятельности
Обеспечить дееспособность и развитие уникального проекта для помощи семьям с детьми инвалидами.
Помочь семьям справиться с такой сложной проблемой, как адаптация своих особых детей вне специальных учреждения.Что мы любим и умеем делать
(наши возможности и ресурсы)
О социальном проекте:
«Поддерживающее проживание»Столярная мастерская
Идей и проб было немало. Это и питомник, где они могли бы помогать в уходе за растениями, и ферма, где они уже неоднократно пробовались на роль подсобных рабочих, ухаживающих за животными.Традиционные рукоделия и ремёсла
О фольклоре, обрядах и играх
Ферма и молочное производство
Жизнь в сельской общине
Автор: Effortless Lesson
-
Дела села Давыдово, жизнь в традициии
ДЕЛА СЕЛАТри цели нашей хозяйственной деятельности
О социальном проекте:
«Поддерживающее проживание»О фольклоре, обрядах и играх
Жизнь в сельской общине
-
Поддерживающее проживание в Давыдово
Видео-презентация
Наш инстаграм
Подписывайтесь, чтобы быть в курсе событий села Давыдово, о людях, о мастерах, о том что и как мы делаем и что у нас из всего этого получается. Как мы живём, чего хотим… и о многом другом
-

Третий принцип методики Хейни
Двенадцать принципов методики Хейни
Милан Хейни (Milan Hejný) — Чешский и Словацкий математик
-
- ПОСТРОЕНИЕ СХЕМ: ребенок знает даже и то, чему мы его не учили
- РАБОТА С ДИДАКТИЧЕСКИМИ БЛОКАМИ: обучение при повторных визитах
- ПЕРЕПЛЕТЕНИЕ ТЕМ: математические законы не изолируются друг от друга
- ПЕРСОНАЛЬНОЕ РАЗВИТИЕ: поощрение самостоятельного мышления детей
- РЕАЛЬНАЯ МОТИВАЦИЯ: когда «я не знаю» и «я хочу знать»
- РЕАЛЬНЫЙ ОПЫТ: обучение на собственном опыте ребёнка
- РАДОСТЬ ОТ МАТЕМАТИКИ: серьёзно помогает в дальнейшем обучении
- СОБСТВЕННЫЕ ОТКРЫТИЯ: вес собственных открытий больше, чем чужих
- РОЛЬ УЧИТЕЛЯ: проводник и ведущий обсуждений
- РАБОТА С ОШИБКОЙ: предотвращение ненужного страха у детей
- АДЕКВАТНАЯ СЛОЖНОСТЬ: для каждого ребенка отдельно в зависимости от его уровня
автор: Милан ХЕЙНИ
перевод с чешского: Светлана ФРИГАТретий ПРИНЦИП. Переплетение тем: математические законы не изолируются друг от другаИнформация не передаётся детям отдельно, она всегда хранится в знакомой схеме, которую ребёнок может вспомнить в любое время. Мы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Наталья Ивановна, мы проходили это две недели назад, мы этого уже не помним…»
Когда мы соотносим отдельные темы в контексте, который соответствует нашему собственному опыту, нам легче вывести и вспомнить знания в любое время. И наоборот, если мы узнаем отдельные факты или правила в изоляции без реального понимания, мы не сможем вспомнить их с течением времени.
Когда информация логически связана
Если бы схему нашей квартиры мы учили так, что в сентябре мы обсудим окна, в октябре кухня, в ноябре ковры и в декабре освещения, то в январе мы должны будем повторить всё, что мы уже об окнах, кухне и коврах забыли. Но поскольку мы узнаем нашу квартиру непосредственно в действии, в повседневной деятельности, которая сочетается и переплетается по-разному, мы можем вспомнить всю квартиру и её части в любое время.
Происходят процессы при которых мы действуем. Действия естественно переплетаются в различных областях нашей квартиры, связывая несколько подсхем. Например вывешивание картин в гостиной — это занятие, которое переплетается со схемами гостиной и окон. Перед тем, как повесить картины, мы рассмотрим, где их будет освещать дневной свет, затем искусственное освещение, а также то, как картинка будет гармонировать с другими украшениями в гостиной и т.д. Мы хорошо знаем нашу квартиру, её отдельные области, хотя мы никогда не учили их. Вся эта информация хранится в диаграмме квартиры, и мы почти всегда можем её запомнить, хотя это может занять некоторое время.
Различные схемы облегчают понимание
Нечто подобное происходит и в методике Хейни. В различных средах или задачах мы определяем отдельные концепции, процессы, стратегии решения, явления, отношения, и их хорошее понимание происходит путем объединения частей мозаики частичных знаний из отдельных дидактических блоков и из различных видов деятельности.
Вот два примера. В первом из них мы покажем, как один вид деятельности смешивается во многих областях. Во втором мы опишем, сколько разных видов деятельности способствуют созданию одного знания.
1. СКЛАДЫВАНИЕ ЛИСТА БУМАГИ
В очень простом упражнении, например, сворачивании квадратного листа бумаги в два одинаковых треугольника, дети используют свой опыт для создания:
- геометрические понятия — квадрат, треугольник, прямоугольный равнобедренный треугольник, диагональ квадрата, вершина и сторона квадрата и треугольника, гипотенуза прямоугольного треугольника, содержание (квадрат может состоять из двух треугольников);
- геометрические отношения — тождество треугольников, квадрат можно разделить на два равнобедренных прямоугольника и наоборот, тождество сторон квадрата и треугольника, диагональ квадрата длиннее его стороны;
- арифметические термины — число 2, т.е. два треугольника; дробь как часть целого, то есть половина квадрата.
Обращаясь и пытаясь сложить бумагу, дети также развивают мелкую моторику, которая позже будет использована при конструировании. Это основная идея задач, предлагаемых детям в разных средах — решая задачи, ребенок не только проявляет свои расчетные навыки, но и распознает что-то иное, нежели фокус задачи. Каждая среда приносит что-то конкретное в математику.
Дети также развивают мелкую моторику при манипулировании и попытке сложить бумагу как можно точнее, это будет использоваться позже в проектных задачах. Это существенная идея задач, предлагаемых детям в разных заданиях – решая задачи, ребёнок не только тренирует свои математические навыки, но познает … и что-то другое, чем то на что работа непосредственно направлена. Каждый дидактический блок привносит что-то особенное в изучение математики.
2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В РАЗЛИЧНЫХ ДИДАКТИЧЕСКИХ БЛОКАХ
Во втором примере давайте посмотрим на сложение и вычитание, и как ребенок может идентифицировать эти простые операции везде:
- при играх и работе с блоком ШАГИ и ЛЕСТНИЦА (шагание, хлопанье в ладоши, повторение чисел, шагание по стрелкам);
- при игре и решении задач по дидактическому блоку АВТОБУС (пассажиры садятся в автобус и выходят из него); (видео)
- работа с ЖИВОТНЫМИ ДЕДУШКИ ЛЕСОНА (создание команд равной силы);
- в ПАУТИНЕ и многих других блоках, где уже играют роль только числа (структурные блоки);
- в геометрических блоках, которые не сосредоточены на арифметических операциях, таких как ПАРКЕТ (выбор паркета, необходимого для покрытия данного пола), ДЕРЕВЯННЫЕ ПАЛОЧКИ (взять три палочки, чтобы сформировать треугольник, взять еще два и создать два треугольника), кубические здания (построить конструкцию так, чтобы было три куба на первом этаже и два на втором этаже) и т. д.
Каждый из этих дидактических блоков по-своему способствует пониманию концепции числа и простых операций сложения и вычитания. Более того, это создает условия для различных стратегий решения.
Примеры дидактических блоков:
алгеброграммы
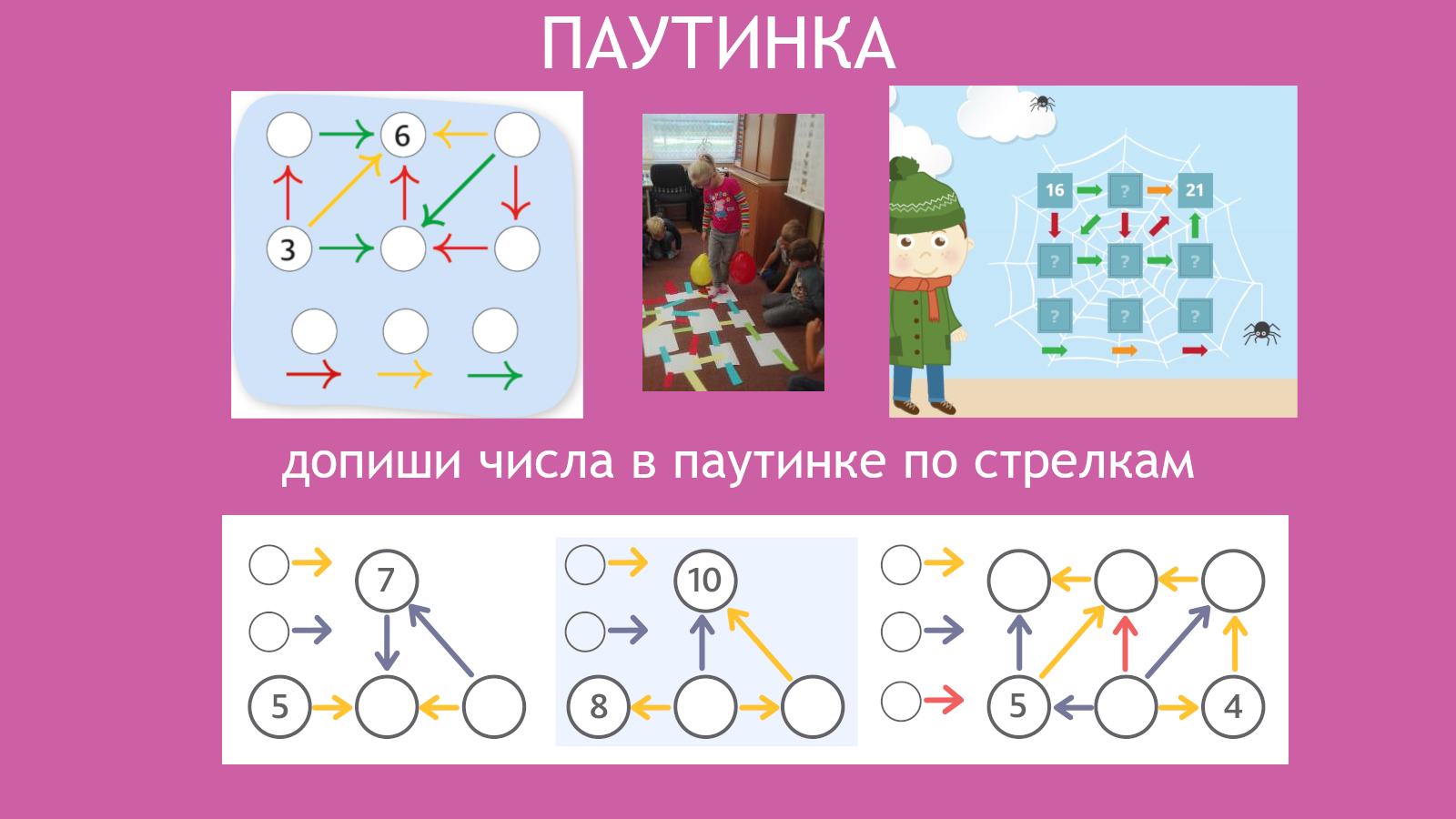
паутинка
змейки
суммарные треугольники
квадраты умножения
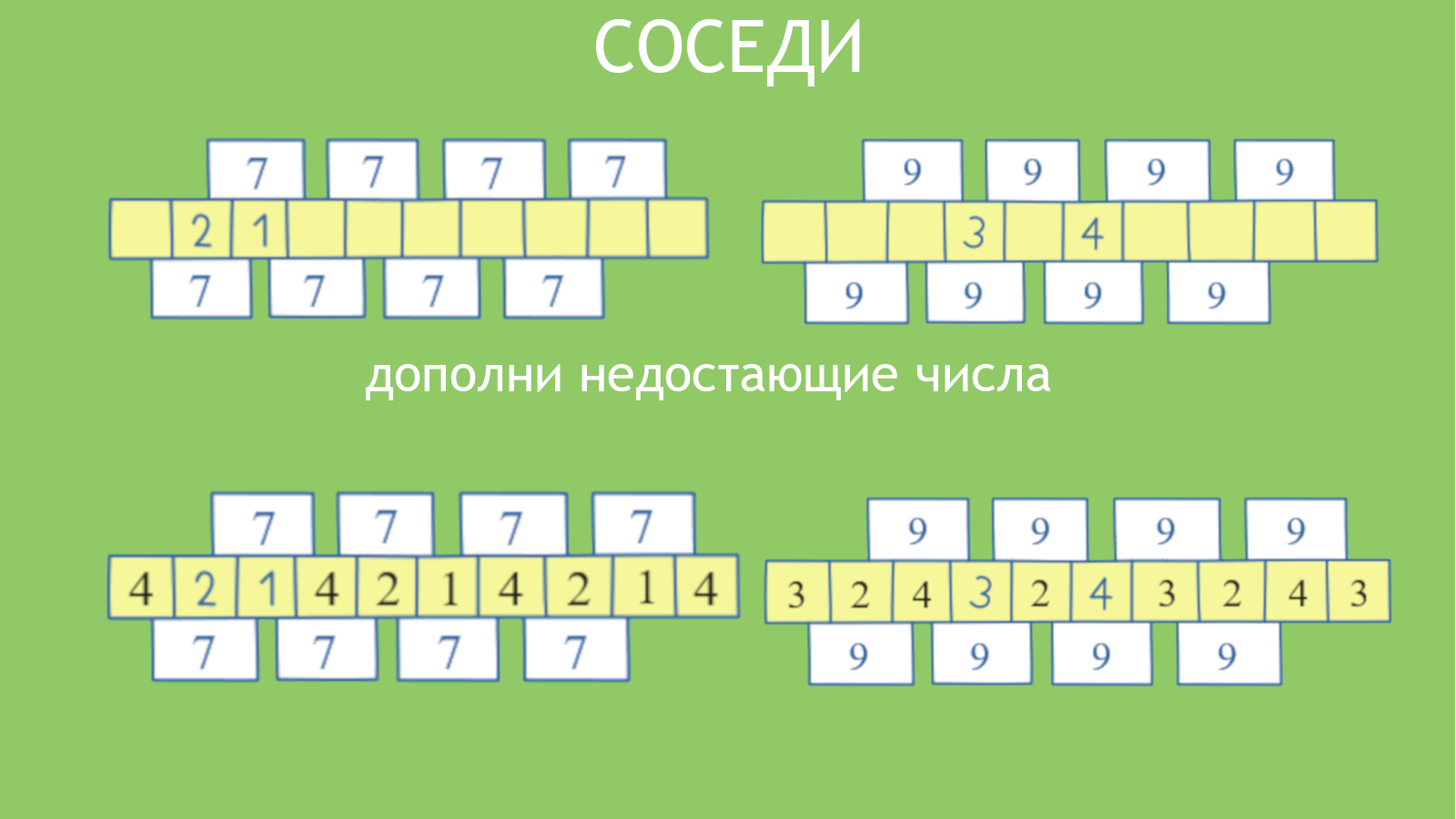
соседи
зверушки лешего
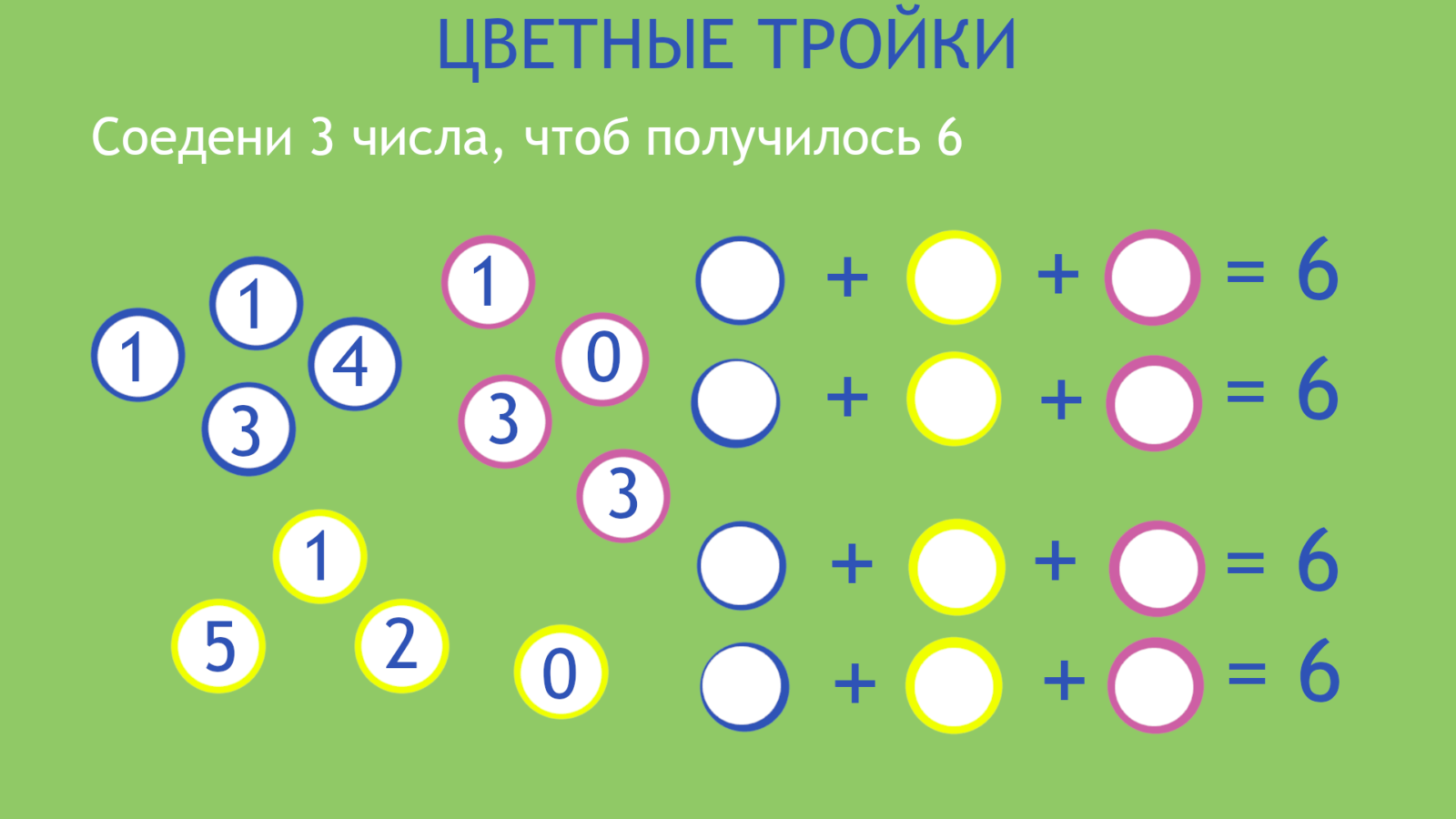
цветная тройка или непоседа

Выйди к доске — и пусть на тебя все посмотрят
Почему некоторые дети не могут заговорить, даже если знают ответ
Есть дети (и подростки), которые отлично знают ответ на вопрос, но не могут сказать его вслух. Не потому что ленятся или стесняются. А потому что буквально замирают.
План организации и проведения Театра теней. Занятие с детьми 3-6 лет в детском саду
нет комментариевТеатр теней с детьми в детском саду
(методическое пособие для занятий с дошкольниками)
\формат для скачивания: PDF
объем: 14 страниц
тема №1: Интеграция двигательно-коммуникативного стиля обучения в онлайн среду начальной школы (приёмы, обоснование, технические возможности) для школьного и семейного обучения
нет комментариевКогда все эти подготовительные действия делаются регулярно, на них уходит очень мало времени, но они создают настрой и благоприятную среду.

Дружное эхо
нет комментариевДружное эхо можно использовать в разных моментах урока. Универсальная игровая разминка. Для незнакомых групп, большой и малой аудитории. Легко проводить.
-
-
12 принципов методики Хейни
Методика Хейни основана на соблюдении 12 основных принципов, которые гениально сложены в целостную концепцию так, чтобы дети открывали математику сами с удовольствием. Методика основывается на 40-летних экспериментах и практически использует исторические знания, которые появлялись в истории математики с Древнего Египта и до наших дней.Первый ПРИНЦИП. Построение схем
Ребёнок знает и то, чему мы его не учили
Вы знаете, сколько окон в вашей квартире? Не наизусть … но если подумать, ответите через некоторое время. И правильно. Потому что у вас в голове есть схема вашей квартиры. У детей также есть схемы в их головах. Метод Хейни позволяет укрепить их, связывает друг с другом и выводит из них общие принципы. Это одна из причин, по которой дети поймут, что половина — это тоже число (0,5), или, например, у них нет проблем с очень «проблемными» дробями.Больше о принципе >
Второй ПРИНЦИП. Работа с дидактическими блоками
Обучение при повторениях
Когда детям знаком какой-либо блок с заданиями, в котором они чувствуют себя хорошо, то они не отвлекаются на незнакомые вещи. Они полностью сосредоточены только на задачи и не отвлекаются на незнакомые данные. Каждый из примерно 25 используемых дидактических блоков работают по-разному (семья, автобус, шаги…). Система блоков мотивационно настроена на охват всех стилей обучения и функционирования детского ума и на дальнейшие эксперименты.Больше о принципе >
Третий ПРИНЦИП. Переплетение тем
Математические законы не изолируются друг от друга
Информация не передаётся детям отдельно, она всегда хранится в знакомой схеме, которую ребёнок может вспомнить в любое время. Мы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Наталья Ивановна, мы проходили это две недели назад, мы этого уже не помним…»Больше о принципе >
Четвёртый ПРИНЦИП. Персональное развитие
Поощрение самостоятельного мышления детей
Одним из главных мотивов профессора Хейни в создании новой методики был акцент на том, чтобы дети не манипулировали в своей жизни. Поэтому учитель при обучении не передает готовые знания, а учит детей в первую очередь спорить, обсуждать и оценивать. Тогда дети сами знают, что для них правильно, уважают другого и умеют принимать решения. Они отважно несут последствия своих действий. В дополнение к математике они, естественно, также открывают основы социального поведения и морально развиваются.Больше о принципе >
Пятый ПРИНЦИП. Реальная мотивация
Когда «я не знаю» и «я хочу знать»
Все математические задачи в методике Хейни построены таким образом, что их решение автоматически «развлекает» детей. Правильная мотивация — внутренняя, а не навязанная извне. Дети приходят к решению задач своими силами. Мы не крадем у детей радость собственного успеха. Благодаря коллегиальной атмосфере в классе аплодисменты получают все — даже те, кто приходит к пониманию или решению позже.Больше о принципе >
Шестой ПРИНЦИП. Реальный опыт
Обучение на собственном опыте ребёнка
Мы используем собственный опыт ребенка, который он накопил с самого первого дня своей жизни — дома, с родителями, при изучении мира вне дома или в песочнице с другими детьми. Мы опираемся на естественный конкретный опыт, из которого ребенок может затем сделать общий вывод. Например, дети «шьют одежду» для куба, автоматически узнавая, сколько стенок у куба, сколько вершин, как рассчитать его поверхность…Больше о принципе >
Седьмой ПРИНЦИП. Радость от математики
Серьёзно помогает в дальнейшем обучении
По опыту ясно: самая эффективная мотивация исходит от чувства успеха ребенка, от его искренней радости, от того, насколько хорошо он решил достаточно сложную задачу. Это радость собственного прогресса и признательность одноклассников и учителей. Детям незнакомы «математические блоки», о которых уже ходят легенды в чешской системе образования. Но, когда они видят формулу, их реакция — не отвращение, а энтузиазм: «я знаю, что я это решу!»Больше о принципе >
Восьмой ПРИНЦИП. Собственные открытия
Вес собственных открытий больше, чем чужих
Когда первоклассник строит квадрат из деревянных брусков, он берет один брусок, затем второй, третий… Ему всё еще не хватает, поэтому он берет четвертый брусок и получается квадрат. Затем он решает надстроить квадрат по высоте. Тогда он берет несколько брусков и надстраивает квадрат. Он уже начинает догадываться, что если он хочет построить ещё один ряд квадрата, то ему всегда нужно взять ещё четыре бруска. Так он встаёт на путь к открытию формулы для расчета периметра квадрата.Больше о принципе >
Девятый ПРИНЦИП. Роль учителя
Проводник и ведущий обсуждений
Привычная социальная идея учителя — это образ человека, который знает, умеет и учит. Таким образом, учитель математики знает математику, поэтому он может о ней говорить. Во многих случаях это так и делается. Ребёнок слышит интерпретацию учителя, записывает некоторые заметки в рабочую тетрадь, слушает объяснение учителя, а потом учится использовать. В нашем понимании преподавания математики, роль учителя и ребенка совершенно иная.Больше о принципе >
Десятый ПРИНЦИП. Работа с ошибкой
Предотвращение ненужного страха у детей
Ребенок, которому запрещено падать, никогда не научится ходить. Анализ ошибок приводит к более глубокому опыту, благодаря которому дети могут лучше запомнить свои знания. Ошибки используются как средство обучения. Мы поощряем детей самим находить ошибки и учим их объяснять, почему они допустили ошибку. Взаимное доверие между ребёнком и учителем способствует радости учеников от проделанной работы.Больше о принципе >
Одиннадцатый ПРИНЦИП. Адекватная сложность
Для каждого ребенка отдельно в зависимости от его уровня
Учебники методики Хейни содержат задания всех уровней сложности. Поскольку слабые ученики всегда решают некоторые задачи, это предотвращают чувство тревоги и ужаса на следующих уроках математики. В то же время перед сильными учениками постоянно ставятся дополнительные проблемы, чтобы они не скучали. Учитель не перегружает задания, но задаёт так, чтобы постоянно мотивировать детей. Он делит задачи в классе в соответствии с потребностями ребенка.
Больше о принципе >
Двенадцатый ПРИНЦИП. Поддержка сотрудничества
Знание рождается через обсуждение
Дети не ждут, пока результат появится на доске. Они работают в группах, парами или даже самостоятельно. Таким образом, каждый учащийся может рассказать, как он / она пришёл к результату, и объяснить его другим. Результат рождается на основе совместной работы. Преподаватель не является здесь абсолютным авторитетом, чтобы просто сказать, где истина, — и переворачивает следующий лист учебника. Ученики строят свои собственные полноценные знания, о которых они постоянно думают.Больше о принципе >
Своевременная консультация позволит заложить основу между учителями и учениками для плодотворного сотрудничества, исправить и спасти сложные ситуации, найти выход из тупиковых ситуаций, преодолеть профессиональное выгорание, найти свой стиль в педагогическом искусстве и поможет не «наломать дров»
Кубические здания
нет комментариевКубические здания. Приём из методики Хейни. Математика интересна и любима детьми, если им дают возможность самим её для себя открывать.

Двенадцатый принцип методики Хейни
нет комментариевДети не ждут, пока результат появится на доске. Они работают в группах, парами или даже самостоятельно. Таким образом, каждый учащийся может рассказать, как он / она пришёл к результату, и объяснить его другим. Результат рождается на основе совместной работы. Преподаватель не является здесь абсолютным авторитетом, чтобы просто сказать, где истина, — и переворачивает следующий лист учебника. Ученики строят свои собственные полноценные знания, о которых они постоянно думают.

Одиннадцатый принцип методики Хейни
нет комментариевУчебники методики Хейни содержат задания всех уровней сложности. Поскольку слабые ученики всегда решают некоторые задачи, это предотвращают чувство тревоги и ужаса на следующих уроках математики. В то же время перед сильными учениками постоянно ставятся дополнительные проблемы, чтобы они не скучали. Учитель не перегружает задания, но задаёт так, чтобы постоянно мотивировать детей. Он делит задачи в классе в соответствии с потребностями ребенка.

Десятый принцип методики Хейни
нет комментариевРебенок, которому запрещено падать, никогда не научится ходить. Анализ ошибок приводит к более глубокому опыту, благодаря которому дети могут лучше запомнить свои знания. Ошибки используются как средство обучения. Мы поощряем детей самим находить ошибки и учим их объяснять, почему они допустили ошибку. Взаимное доверие между ребёнком и учителем способствует радости учеников от проделанной работы.

Девятый принцип методики Хейни
нет комментариевПривычная социальная идея учителя — это образ человека, который знает, умеет и учит. Таким образом, учитель математики знает математику, поэтому он может о ней говорить. Во многих случаях это так и делается. Ребёнок слышит интерпретацию учителя, записывает некоторые заметки в рабочую тетрадь, слушает объяснение учителя, а потом учится использовать. В нашем понимании преподавания математики, роль учителя и ребенка совершенно иная.

Восьмой принцип методики Хейни
нет комментариевКогда первоклассник строит квадрат из деревянных брусков, он берет один брусок, затем второй, третий… Ему всё еще не хватает, поэтому он берет четвертый брусок и получается квадрат. Затем он решает надстроить квадрат по высоте. Тогда он берет несколько брусков и надстраивает квадрат. Он уже начинает догадываться, что если он хочет построить ещё один ряд квадрата, то ему всегда нужно взять ещё четыре бруска. Так он встаёт на путь к открытию формулы для расчета периметра квадрата.

Седьмой принцип методики Хейни
нет комментариевПо опыту ясно: самая эффективная мотивация исходит от чувства успеха ребенка, от его искренней радости, от того, насколько хорошо он решил достаточно сложную задачу. Это радость собственного прогресса и признательность одноклассников и учителей. Детям незнакомы «математические блоки», о которых уже ходят легенды в чешской системе образования. Но, когда они видят формулу, их реакция — не отвращение, а энтузиазм: «я знаю, что я это решу!»

Шестой принцип методики Хейни
нет комментариевМы используем собственный опыт ребенка, который он накопил с самого первого дня своей жизни — дома, с родителями, при изучении мира вне дома или в песочнице с другими детьми. Мы опираемся на естественный конкретный опыт, из которого ребенок может затем сделать общий вывод. Например, дети «шьют одежду» для куба, автоматически узнавая, сколько стенок у куба, сколько вершин, как рассчитать его поверхность…

Пятый принцип методики Хейни
нет комментариевВсе математические задачи в методике Хейни построены таким образом, что их решение автоматически «развлекает» детей. Правильная мотивация — внутренняя, а не навязанная извне. Дети приходят к решению задач своими силами. Мы не крадем у детей радость собственного успеха. Благодаря коллегиальной атмосфере в классе аплодисменты получают все — даже те, кто приходит к пониманию или решению позже.

Четвёртый принцип методики Хейни
нет комментариевОдним из главных мотивов профессора Хейни в создании новой методики был акцент на том, чтобы дети не манипулировали в своей жизни. Поэтому учитель при обучении не передает готовые знания, а учит детей в первую очередь спорить, обсуждать и оценивать. Тогда дети сами знают, что для них правильно, уважают другого и умеют принимать решения. Они отважно несут последствия своих действий. В дополнение к математике они, естественно, также открывают основы социального поведения и морально развиваются.

Сценарий применения дидактического блока АВТОБУС
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

АВТОБУС (дидактический блок методики Хейни) — описание
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

Третий принцип методики Хейни
нет комментариевМы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Мы проходили это две недели назад, мы этого уже не помним…»
12 принципов методики Хейни
Методика Хейни основана на соблюдении 12 основных принципов, которые гениально сложены в целостную концепцию так, чтобы дети открывали математику сами с удовольствием. Методика основывается на 40-летних экспериментах и практически использует исторические знания, которые появлялись в истории математики с Древнего Египта и до наших дней.
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика для дошкольников, учеников начальных, средних и старших классов общеобразовательных школ
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни)
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни) — учебные задания для обучения математики в начальных классах по методике чешского математика Хейни

2 принцип методики Хейни (чешская методика обучения математике в начальных классах)
нет комментариевДидактические блоки способствуют получению неформальных знаний. 2 Принцип методики обучения математики в начальных классах. Никакого страха перед математикой. Дети, выполняя задания сами не замечают, что они работают, для них это интересная игра.

1 принцип метода Хейни (чешская методика обучения математике в начальных классах)
нет комментариевЧешская методика обучения математике детей в начальной школе. Основана на создание рабочей среды на образах и схемах детей. Методика Хейни

Преподавание математики по Хейни: То, что дети узнают сами, никогда не забудут
нет комментариевМетодика Хейни. Игровая образно-наглядная чешская методика по обучению математике в начальных классах.
-
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика
автор методики: Милан Хейни
математика для дошкольников, учеников начальных, средних и старших классов общеобразовательных школ

Кубические здания
нет комментариевКубические здания. Приём из методики Хейни. Математика интересна и любима детьми, если им дают возможность самим её для себя открывать.

Двенадцатый принцип методики Хейни
нет комментариевДети не ждут, пока результат появится на доске. Они работают в группах, парами или даже самостоятельно. Таким образом, каждый учащийся может рассказать, как он / она пришёл к результату, и объяснить его другим. Результат рождается на основе совместной работы. Преподаватель не является здесь абсолютным авторитетом, чтобы просто сказать, где истина, — и переворачивает следующий лист учебника. Ученики строят свои собственные полноценные знания, о которых они постоянно думают.

Одиннадцатый принцип методики Хейни
нет комментариевУчебники методики Хейни содержат задания всех уровней сложности. Поскольку слабые ученики всегда решают некоторые задачи, это предотвращают чувство тревоги и ужаса на следующих уроках математики. В то же время перед сильными учениками постоянно ставятся дополнительные проблемы, чтобы они не скучали. Учитель не перегружает задания, но задаёт так, чтобы постоянно мотивировать детей. Он делит задачи в классе в соответствии с потребностями ребенка.

Десятый принцип методики Хейни
нет комментариевРебенок, которому запрещено падать, никогда не научится ходить. Анализ ошибок приводит к более глубокому опыту, благодаря которому дети могут лучше запомнить свои знания. Ошибки используются как средство обучения. Мы поощряем детей самим находить ошибки и учим их объяснять, почему они допустили ошибку. Взаимное доверие между ребёнком и учителем способствует радости учеников от проделанной работы.

Девятый принцип методики Хейни
нет комментариевПривычная социальная идея учителя — это образ человека, который знает, умеет и учит. Таким образом, учитель математики знает математику, поэтому он может о ней говорить. Во многих случаях это так и делается. Ребёнок слышит интерпретацию учителя, записывает некоторые заметки в рабочую тетрадь, слушает объяснение учителя, а потом учится использовать. В нашем понимании преподавания математики, роль учителя и ребенка совершенно иная.

Восьмой принцип методики Хейни
нет комментариевКогда первоклассник строит квадрат из деревянных брусков, он берет один брусок, затем второй, третий… Ему всё еще не хватает, поэтому он берет четвертый брусок и получается квадрат. Затем он решает надстроить квадрат по высоте. Тогда он берет несколько брусков и надстраивает квадрат. Он уже начинает догадываться, что если он хочет построить ещё один ряд квадрата, то ему всегда нужно взять ещё четыре бруска. Так он встаёт на путь к открытию формулы для расчета периметра квадрата.

Седьмой принцип методики Хейни
нет комментариевПо опыту ясно: самая эффективная мотивация исходит от чувства успеха ребенка, от его искренней радости, от того, насколько хорошо он решил достаточно сложную задачу. Это радость собственного прогресса и признательность одноклассников и учителей. Детям незнакомы «математические блоки», о которых уже ходят легенды в чешской системе образования. Но, когда они видят формулу, их реакция — не отвращение, а энтузиазм: «я знаю, что я это решу!»

Шестой принцип методики Хейни
нет комментариевМы используем собственный опыт ребенка, который он накопил с самого первого дня своей жизни — дома, с родителями, при изучении мира вне дома или в песочнице с другими детьми. Мы опираемся на естественный конкретный опыт, из которого ребенок может затем сделать общий вывод. Например, дети «шьют одежду» для куба, автоматически узнавая, сколько стенок у куба, сколько вершин, как рассчитать его поверхность…

Пятый принцип методики Хейни
нет комментариевВсе математические задачи в методике Хейни построены таким образом, что их решение автоматически «развлекает» детей. Правильная мотивация — внутренняя, а не навязанная извне. Дети приходят к решению задач своими силами. Мы не крадем у детей радость собственного успеха. Благодаря коллегиальной атмосфере в классе аплодисменты получают все — даже те, кто приходит к пониманию или решению позже.

Четвёртый принцип методики Хейни
нет комментариевОдним из главных мотивов профессора Хейни в создании новой методики был акцент на том, чтобы дети не манипулировали в своей жизни. Поэтому учитель при обучении не передает готовые знания, а учит детей в первую очередь спорить, обсуждать и оценивать. Тогда дети сами знают, что для них правильно, уважают другого и умеют принимать решения. Они отважно несут последствия своих действий. В дополнение к математике они, естественно, также открывают основы социального поведения и морально развиваются.

Сценарий применения дидактического блока АВТОБУС
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

АВТОБУС (дидактический блок методики Хейни) — описание
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

Третий принцип методики Хейни
нет комментариевМы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Мы проходили это две недели назад, мы этого уже не помним…»
12 принципов методики Хейни
Методика Хейни основана на соблюдении 12 основных принципов, которые гениально сложены в целостную концепцию так, чтобы дети открывали математику сами с удовольствием. Методика основывается на 40-летних экспериментах и практически использует исторические знания, которые появлялись в истории математики с Древнего Египта и до наших дней.
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика для дошкольников, учеников начальных, средних и старших классов общеобразовательных школ
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни)
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни) — учебные задания для обучения математики в начальных классах по методике чешского математика Хейни

2 принцип методики Хейни (чешская методика обучения математике в начальных классах)
нет комментариевДидактические блоки способствуют получению неформальных знаний. 2 Принцип методики обучения математики в начальных классах. Никакого страха перед математикой. Дети, выполняя задания сами не замечают, что они работают, для них это интересная игра.

1 принцип метода Хейни (чешская методика обучения математике в начальных классах)
нет комментариевЧешская методика обучения математике детей в начальной школе. Основана на создание рабочей среды на образах и схемах детей. Методика Хейни

Преподавание математики по Хейни: То, что дети узнают сами, никогда не забудут
нет комментариевМетодика Хейни. Игровая образно-наглядная чешская методика по обучению математике в начальных классах.
-
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни)
учебные задания для обучения математики в начальных классах по методике чешского математика Хейни
Абаку
Основной целью блока Абаку является укрепление числовых (расчетных) соединений. Это соединения типа 2 + 3 = 5, 4 + 6 = 10, таблица умножения и др. Если ученик создаст соединения такого типа, то в будущем ему это облегчает работу в более сложных математических темах, например, при расширении и сокращение дроби. Важно, чтобы ученики делали это с интересом, чтобы они не чувствовали скуку, чтобы это их занимало.
Начинать в последней трети первого класса.
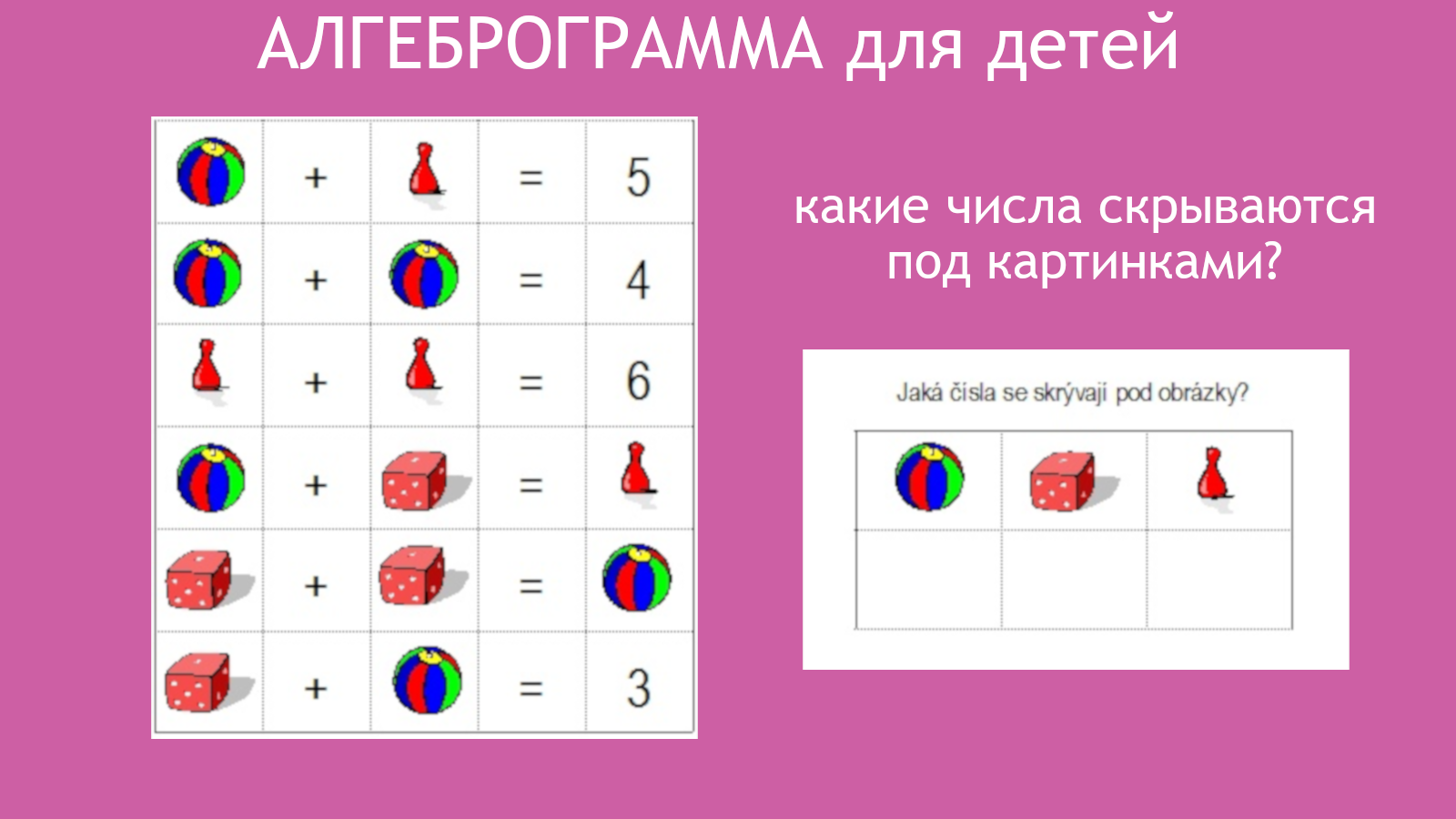
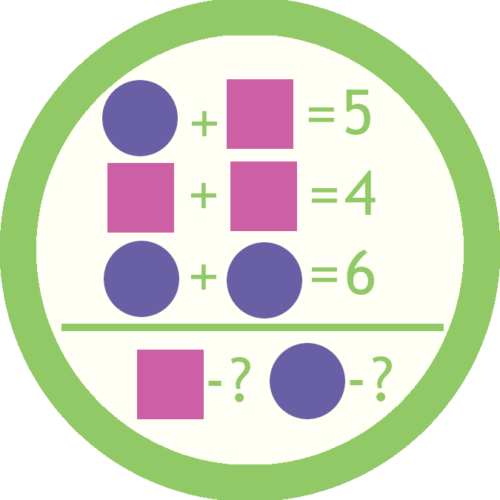
Алгеброграммы и звездограммы
Алгеброграммы строят понимание десятичной системы и позволяют выявить более глубокие связи арифметики. Они также развивают комбинаторное мышление и способность рассуждать.
Автобус
Методическое описание
Сценарий применения дидактического блока АВТОБУС
Видео про дидактический блок АВТОБУСДидактический блок (игра) в которой используются знакомые детям объекты и пространство, для удовольствия и приобретения собственного опыта. На этот приём можно опираться при обучении в школе и в подготовительной группе детского сада.
Автобусные линии
Местность обозначается пунктом в графической схеме, а путь между является линией графика. В задачах появляются комбинаторные ситуации или задачи, направленные на деление (наименьший общий делитель числа, …).
Разноцветные тройки
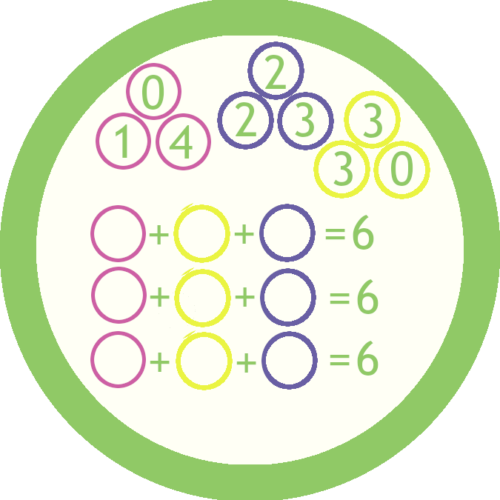
Этот дидактический блок для освоения и углубления базовых арифметических знаний, комбинаторного мышления и стратегии.
Циферблат
Циферблат-это элементарный инструмент. Прежде всего, он предназначен для определения времени, но мы можем использовать его для других видов деятельности по математике, геометрии и т.д.
Кубические здания
Этот дидактический блок опирается на опыт детей игры с кубиками, легко интегрируется в процесс изучения арифметики и очень способствует развитию пространственного воображения.
источник: Didaktická prostředí

Кубические здания
нет комментариевКубические здания. Приём из методики Хейни. Математика интересна и любима детьми, если им дают возможность самим её для себя открывать.

Двенадцатый принцип методики Хейни
нет комментариевДети не ждут, пока результат появится на доске. Они работают в группах, парами или даже самостоятельно. Таким образом, каждый учащийся может рассказать, как он / она пришёл к результату, и объяснить его другим. Результат рождается на основе совместной работы. Преподаватель не является здесь абсолютным авторитетом, чтобы просто сказать, где истина, — и переворачивает следующий лист учебника. Ученики строят свои собственные полноценные знания, о которых они постоянно думают.

Одиннадцатый принцип методики Хейни
нет комментариевУчебники методики Хейни содержат задания всех уровней сложности. Поскольку слабые ученики всегда решают некоторые задачи, это предотвращают чувство тревоги и ужаса на следующих уроках математики. В то же время перед сильными учениками постоянно ставятся дополнительные проблемы, чтобы они не скучали. Учитель не перегружает задания, но задаёт так, чтобы постоянно мотивировать детей. Он делит задачи в классе в соответствии с потребностями ребенка.

Десятый принцип методики Хейни
нет комментариевРебенок, которому запрещено падать, никогда не научится ходить. Анализ ошибок приводит к более глубокому опыту, благодаря которому дети могут лучше запомнить свои знания. Ошибки используются как средство обучения. Мы поощряем детей самим находить ошибки и учим их объяснять, почему они допустили ошибку. Взаимное доверие между ребёнком и учителем способствует радости учеников от проделанной работы.

Девятый принцип методики Хейни
нет комментариевПривычная социальная идея учителя — это образ человека, который знает, умеет и учит. Таким образом, учитель математики знает математику, поэтому он может о ней говорить. Во многих случаях это так и делается. Ребёнок слышит интерпретацию учителя, записывает некоторые заметки в рабочую тетрадь, слушает объяснение учителя, а потом учится использовать. В нашем понимании преподавания математики, роль учителя и ребенка совершенно иная.

Восьмой принцип методики Хейни
нет комментариевКогда первоклассник строит квадрат из деревянных брусков, он берет один брусок, затем второй, третий… Ему всё еще не хватает, поэтому он берет четвертый брусок и получается квадрат. Затем он решает надстроить квадрат по высоте. Тогда он берет несколько брусков и надстраивает квадрат. Он уже начинает догадываться, что если он хочет построить ещё один ряд квадрата, то ему всегда нужно взять ещё четыре бруска. Так он встаёт на путь к открытию формулы для расчета периметра квадрата.

Седьмой принцип методики Хейни
нет комментариевПо опыту ясно: самая эффективная мотивация исходит от чувства успеха ребенка, от его искренней радости, от того, насколько хорошо он решил достаточно сложную задачу. Это радость собственного прогресса и признательность одноклассников и учителей. Детям незнакомы «математические блоки», о которых уже ходят легенды в чешской системе образования. Но, когда они видят формулу, их реакция — не отвращение, а энтузиазм: «я знаю, что я это решу!»

Шестой принцип методики Хейни
нет комментариевМы используем собственный опыт ребенка, который он накопил с самого первого дня своей жизни — дома, с родителями, при изучении мира вне дома или в песочнице с другими детьми. Мы опираемся на естественный конкретный опыт, из которого ребенок может затем сделать общий вывод. Например, дети «шьют одежду» для куба, автоматически узнавая, сколько стенок у куба, сколько вершин, как рассчитать его поверхность…

Пятый принцип методики Хейни
нет комментариевВсе математические задачи в методике Хейни построены таким образом, что их решение автоматически «развлекает» детей. Правильная мотивация — внутренняя, а не навязанная извне. Дети приходят к решению задач своими силами. Мы не крадем у детей радость собственного успеха. Благодаря коллегиальной атмосфере в классе аплодисменты получают все — даже те, кто приходит к пониманию или решению позже.

Четвёртый принцип методики Хейни
нет комментариевОдним из главных мотивов профессора Хейни в создании новой методики был акцент на том, чтобы дети не манипулировали в своей жизни. Поэтому учитель при обучении не передает готовые знания, а учит детей в первую очередь спорить, обсуждать и оценивать. Тогда дети сами знают, что для них правильно, уважают другого и умеют принимать решения. Они отважно несут последствия своих действий. В дополнение к математике они, естественно, также открывают основы социального поведения и морально развиваются.

Сценарий применения дидактического блока АВТОБУС
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

АВТОБУС (дидактический блок методики Хейни) — описание
нет комментариевАвтобус — описание игры, в которой используются знакомые детям объекты и среда, чтобы наслаждаться и получать собственный опыт. На них можно опираться при обучении в школе. Мы делаем автобус из картонной коробки, а пассажиры могут использовать игрушки или пробки из ПЭТ-бутылок.

Третий принцип методики Хейни
нет комментариевМы не разрываем математические явления и понятия друг от друга, но мы задействуем различные стратегии решения. Ребёнок сам выбирает, что ему лучше подходит для решения, что для него естественнее. На уроках вы не услышите такого заявления: «Мы проходили это две недели назад, мы этого уже не помним…»
12 принципов методики Хейни
Методика Хейни основана на соблюдении 12 основных принципов, которые гениально сложены в целостную концепцию так, чтобы дети открывали математику сами с удовольствием. Методика основывается на 40-летних экспериментах и практически использует исторические знания, которые появлялись в истории математики с Древнего Египта и до наших дней.
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика
Чешская МЕТОДИКА ХЕЙНИ (ČR: Hejného metoda) — математика для дошкольников, учеников начальных, средних и старших классов общеобразовательных школ
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни)
ДИДАКТИЧЕСКИЕ БЛОКИ (математика, методика Хейни) — учебные задания для обучения математики в начальных классах по методике чешского математика Хейни

2 принцип методики Хейни (чешская методика обучения математике в начальных классах)
нет комментариевДидактические блоки способствуют получению неформальных знаний. 2 Принцип методики обучения математики в начальных классах. Никакого страха перед математикой. Дети, выполняя задания сами не замечают, что они работают, для них это интересная игра.

1 принцип метода Хейни (чешская методика обучения математике в начальных классах)
нет комментариевЧешская методика обучения математике детей в начальной школе. Основана на создание рабочей среды на образах и схемах детей. Методика Хейни

Преподавание математики по Хейни: То, что дети узнают сами, никогда не забудут
нет комментариевМетодика Хейни. Игровая образно-наглядная чешская методика по обучению математике в начальных классах.
-

133 зайца (обзор)
Второй из трёх социо-игровых постулата педагогического мастерства
В народе как говорят:«За двумя зайцами погонишься — ни одного не поймаешь». Трудно не согласиться! Однако, если«ситуацию» рассмотреть детальнее и вспомнить про социо-игровую вариативность, то дело может представиться несколько иначе. Если уж гнаться,- так не за двумя (или тем более — одним), а сразу за 133-мя зайцами! Тогда, глядишь, с десяток и поймаешь (из которых, вполне возможно, пяток окажется даже еще и «науке неизвестными»!).
Другими словами — наступит нечаянная радость!
И действительно, ведь если учителю весь урок только за одним зайцем гоняться, то КПД (коэффициент полезного действия) будет явно низеньким. А то и вовсе нулевым…
Почему же учителя стараются свои уроки то и дело подгонять под ранжир, строго соблюдая методические предписания? Да все потому, что надеются обеспечить поимку нужного программного «зайца». Хотя известно, что с некоторыми детьми этого самого «зайца» в нужные сроки ну никак не поймаешь!..
Если же учитель отважился вести урок в стиле, например, социо-игровой режиссуры, то при изучении темы, скажем, «Сравнение математических величин», вдруг окажется, что Коля научился-таки слушать других, а Маруся наконец-то поняла, что ей давно пора начать подстраиваться к общему делу. Тогда как их соседу Сашке на том же самом уроке удалось сам смысл новой темы весьма неплохо ухватить…
И прекрасно! Главное, что каждый из детей на том уроке жил не бессмысленно. И хотя деятельность каждого протекала в своем индивидуальном темпо/ритме, у всех она оказалась вполне насыщенной.
Обратим особое внимание — насыщенной у каждого по-своему. А потому для каждого — полноценной. Именно наличие во время урока у каждого ученика этого впечатления «наполненности жизни» гарантирует эмоционально заряженное освоение (то есть индивидуальное понимание) данной учебной темы не только сметливым Сашком, но и окружающими его соседями. Правда, не сразу (как того очень хотелось бы любому из взрослых), а в каком-то более или менее ближайшем (или наоборот отдаленном) будущем. Таков закон человеческой природы, на который учителям было бы глупо пенять…
Хотя от учителей приходится слышать: почему же тогда у них в классе отличница Оля после первого же объяснения знает, как задачку решать, а вот ее соседи решение той же самой задачки ну никак — целую четверть, хоть убей! — в толк взять не могут? В том-то и дело, что раз жизнь у Олиных соседей на уроках протекает не насыщенно, не полноценно (то есть их индивидуальные темпоритмы во время урока оказываются угнетенными, а то и вовсе «придушенными» или «убитыми»), то уж какой тут потенциал? Учителю можно рассчитывать на результат эмоционально-интеллектуальной латентности только при условии, что ученик прожил урок не опустошенным. При этом мерилом смысла той самой насыщенности оказывается не мнение учителя, проводившего урок, а впечатление самого ученика.
Так как же тогда современному учителю свои уроки и планировать, и проводить? И какие же условия (и как?) ему создавать для личностного развития каждого — «здесь-и-сейчас» — присутствующего ребёнка, чтобы каждый из них на одном и том же уроке поймал собственного зайчонка: беленького ли, серенького ли, солнечного ли или какого-то другого?..
Одно из решений — вспомнив о драмогерменевтической процедуре и основываясь на её рекомендациях, строить свою работу с классом так, чтобы главным на уроке стало групповое обживание «текста». Что и обеспечит каждому из присутствующих индивидуальное погружение в изучаемый текст.
Напомним, что в папке с материалами «Диктанта на дружбу» можно найти разъяснение-комментарий психологической связи «обживания текста» с педагогическим постулатом «133 зайца»: когда ученик оказывается один на один с текстом (то есть с культурным реликтом), то этот текст может оказаться ему и не по зубам. А вот когда он в кругу приятелей, когда он чувствует их возрастающий интерес, их дыхание и поток мыслей, когда высказываемые вокруг мнения, материализуясь прямо «на глазах», обретают для него конкретность, становясь фактами биографии, когда партнерское «чувство локтя» начинает помогать ему уверенно карабкаться вверх по «шершавым скалам человеческой культуры», не боясь свернуть себе шею или быть публично осмеянным, — тогда любой реликт для него оказывается не таким уж и страшным, неприступным или чуждым… А подогреваемое соседями любопытство оказывается отличным топливом для начала, продолжения или завершения персонального путешествия – путешествия за своим пониманием (знаниями, мыслями, чувствами, открытиями), то есть за своим личным опытом.
И нам остаётся лишь очередной раз подчеркнуть, что по ходу этих своих образовательный путешествий ученики то и дело будут обретать неожиданные (или наоборот ожидаемые, но недостающие) пазлы самих себя. То есть им то и дело будут приоткрываться мимолётные (но весьма убедительные, а потому и особо ценные) образы своих «идеальных Я»…Так что учителю, озабоченному поиском творческих ответов на подобные профессиональные заморочки, можно посоветовать почаще заглядывать, например, в таблицу-БАБОЧКУ.
-
Три социо-игровых постулата педагогического мастерства
Три социо-игровых постулата педагогического мастерстваОдной из сверхзадач социо-игровой методики создание условий при которых учителю хотелось бы слушать обучаемых детей. Что говорят и думают сами дети, что они сами считают интересным. При привычном «глухом» стиле работы учителя, кажется, что ученик ничего путного сказать не сможет. Справедливости ради следует отметить, что среди учителей есть и те, кто не столько стоит на страже своих профессиональных амбиций, сколько стремится, как-то развиваться, расширяя свой педагогический диапазон в самых разнообразных направлениях. Возможно, включая и интерес к умению «слушать детей»… Именно для поддержки желания учителей саморазвиваться и совершенствоваться в свое время и были сформулированы три социо-игровых постулата педагогического мастерства.1. Не учить!
2. Гнаться за 133 зайцами!
3. Не бояться быть идиотом
-
Социо-игровая технология обучения (обзор)
Социо-игровая педагогическая технология для работы с детьми дошкольного и школьного возраста. Особенности и характеристики: работа малыми группами; движение детей во время занятий; дети в активном общении между собой добывают знания; учитель придерживается роли модератора, а не лектора; не ловить на ошибках; учитель не является носителем истины в последней инстанции; работа через посыльных; игровые правила и ограничения; динамичная смена темпа, ритма, ролей и мизансцен; а также принцип снятия с педагога оценивающей, судейской роли и передача её ученикам.Социо-игровой подход («стиль», «методика», «технология», «режиссура урока») предполагает организацию занятия как игры-жизни между микрогруппами детей (малыми социумами — отсюда и термин «социо-игровая») и одновременно внутри каждой из них. Он основывается на формировании и использовании учениками умений свободно обсуждать интересующие их вопросы, следить за развитием общего разговора и за ходом общего дела, оказывать друг другу помощь и принимать её, когда это нужно.
Представления об особенностях социо-игрового стиля обучения сложились в 1970-е годы в результате объединения двух направлений педагогических исследований:
- экспериментальной практики ровеснического начального образования, создаваемой в 91-й школе г. Москвы сотрудниками Лаборатории младшего школьника НИИ Психологии АПН СССР Е. Е. Шулешко и Л. К. Филякиной;
- адаптации к условиям обычных уроков по любому школьному предмету приёмов театральной педагогики и театральной «теория действий», разработанной П. М. Ершовым на основе системы К. С. Станиславского (чем занимались сотрудники Лаборатории театра Института художественного образования (ИХО) Академии педагогических наук СССР А. П. Ершова и В. М. Букатов).
- В разные годы существенный вклад в разработку социо-игровых подходов вносили учителя-исследователи: Л. К. Филякина, С. В. Плахотников, М. В. Ганькина, Е.А.Аккуратова, Н. В. Жеребилова, Л. П. Аншукова, О. П. Травина и др.
ТРИ ЗОЛОТЫХ ПРАВИЛА
- Двигательная деятельность обучаемых (первое золотое правило)
- Смена мизансцен, ролей, темпо ритма на уроке (второе золотое правило)
- Работа учеников малыми группами (третье золотое правило)
Об особенностях социо-игрового стиля работы школьных учителей
- Воспоминания о будущем
- Сочинять новое или вспоминать старое?
- Об учительских письмах-отчетах
- Парадоксы плодородия или О «трёх китах» социо-игровых технологий
- Драмогерменевтика>>>
- Игровые приёмы обучения>>>
- Режиссура урока>>>
- Азы терминологии>>>
Записи не найдены